Section : Modèles linéaires
Précédent : Exercice 1.
Suivant : Exemples
Soit
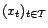 une série
temporelle (univariée, discrète). Une première
approche de la modélisation, dite décomposition
classique, est de supposer qu'il s'agit d'une trajectoire
typique d'un processus
une série
temporelle (univariée, discrète). Une première
approche de la modélisation, dite décomposition
classique, est de supposer qu'il s'agit d'une trajectoire
typique d'un processus
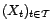 dont on distingue une
partie déterministe et une partie aléatoire :
dont on distingue une
partie déterministe et une partie aléatoire :
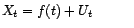
(modèle
additif)
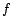 est déterministe, et
est déterministe, et
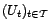 est un processus
aléatoire centré, parfois appelé
résidu aléatoire. Il en résulte
Il est souvent possible de décomposer
est un processus
aléatoire centré, parfois appelé
résidu aléatoire. Il en résulte
Il est souvent possible de décomposer 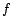 en somme d'une tendance
en somme d'une tendance 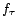 et d'une ou
de plusieurs saisonnalités
et d'une ou
de plusieurs saisonnalités
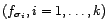 de
périodes différentes :
Une saisonnalité
de
périodes différentes :
Une saisonnalité
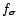 est une fonction périodique
``centrée'' ; si
est une fonction périodique
``centrée'' ; si 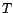 est sa période, alors
elle doit vérifier les deux conditions (en supposant
est sa période, alors
elle doit vérifier les deux conditions (en supposant
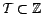 ) :
Remarquons que
) :
Remarquons que  implique
implique 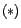 : en
effet, si
: en
effet, si
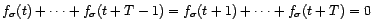 , alors, par soustraction,
, alors, par soustraction,
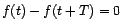 .
.
Opérer une décomposition classique revient donc
à distinguer dans la série initiale trois
phénomènes concommittants :
- une allure régulière, représentée
par la tendance, et caractérisant l'évolution
à moyen et long terme de la série
- des variations à court terme cycliques et
prévisibles, représentées par la
saisonnalité
- une partie erratique, imprévisible,
représentée par le résidu, correspondant aux
aléas des mesures ou des événements
Si
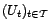 est un bruit blanc, et
si
est un bruit blanc, et
si
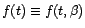 est une fonction
linéaire de son paramètre
est une fonction
linéaire de son paramètre
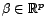 , alors on
reconnaît dans le modèle additif un modèle
linéaire. Sur quelques exemples, nous allons voir comment le
mettre en
, alors on
reconnaît dans le modèle additif un modèle
linéaire. Sur quelques exemples, nous allons voir comment le
mettre en  uvre en pratique, en s'aidant des techniques
de moyennes mobiles pour déterminer
uvre en pratique, en s'aidant des techniques
de moyennes mobiles pour déterminer 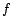 .
.
Sous-sections
Section : Modèles linéaires
Précédent : Exercice 1.
Suivant : Exemples
Thierry Cabanal-Duvillard
![]() une série
temporelle (univariée, discrète). Une première
approche de la modélisation, dite décomposition
classique, est de supposer qu'il s'agit d'une trajectoire
typique d'un processus
une série
temporelle (univariée, discrète). Une première
approche de la modélisation, dite décomposition
classique, est de supposer qu'il s'agit d'une trajectoire
typique d'un processus
![]() dont on distingue une
partie déterministe et une partie aléatoire :
dont on distingue une
partie déterministe et une partie aléatoire :
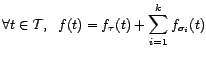
![]() est un bruit blanc, et
si
est un bruit blanc, et
si
![]() est une fonction
linéaire de son paramètre
est une fonction
linéaire de son paramètre
![]() , alors on
reconnaît dans le modèle additif un modèle
linéaire. Sur quelques exemples, nous allons voir comment le
mettre en
, alors on
reconnaît dans le modèle additif un modèle
linéaire. Sur quelques exemples, nous allons voir comment le
mettre en ![]() uvre en pratique, en s'aidant des techniques
de moyennes mobiles pour déterminer
uvre en pratique, en s'aidant des techniques
de moyennes mobiles pour déterminer ![]() .
.