Section : Exemples
Précédent : Coefficient de détermination.
Suivant : Transport aérien
Pendant six années, on a relevé mensuellement la
mortalité accidentelle aux États-Unis :
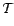 |
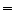 |
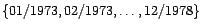 |
|
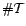 |
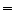 |
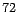 |
|
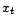 |
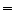 |
nombre de décès accidentels
durant le mois 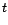 |
|
On observe à l'évidence un comportement saisonnier
de la série, reflet prévisible des variations
saisonnières des activités humaines. On se propose
donc de construire un modèle de la forme
avec
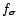 saisonnalité de
période 12 mois, et
saisonnalité de
période 12 mois, et
 bruit blanc faible. Pour
estimer la tendance
bruit blanc faible. Pour
estimer la tendance 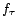 , on peut utiliser
encore la méthode des moyennes mobiles, mais en faisant la
remarque suivante : comme
, on peut utiliser
encore la méthode des moyennes mobiles, mais en faisant la
remarque suivante : comme
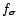 est une saisonnalité de
période
est une saisonnalité de
période 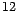 , alors
ce qui implique
On en déduit que
, alors
ce qui implique
On en déduit que
On élimine ainsi la partie saisonnière de la
tendance, et l'on est ramené aux situations
précédentes. Cette astuce peut évidemment
s'adapter à toute saisonnalité, quelle que soit sa
période, en distinguant entre période paire et
impaire.
Au vu de cette estimation de 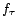 , on fait
l'hypothèse d'un comportement parabolique. On est ainsi
ramené au modèle linéaire suivant
, on fait
l'hypothèse d'un comportement parabolique. On est ainsi
ramené au modèle linéaire suivant
avec 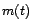 le mois correspondant à la date
le mois correspondant à la date
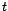 . Il s'agit donc d'un modèle qui
mêle régression à deux facteurs et analyse de
la variance à un facteur. On parle alors de modèle
d'analyse de la covariance. Les valeurs prises par les estimateurs
des moindres carrés, après application
numérique, sont :
Remarquons que pour chacun de ces coefficients on peut effectuer un
test de nullité, et ôter du modèle ceux qui ne
sont pas significativement différents de zéro. Il va
de soi que l'on préfère avoir le moins de
paramètres possible.
. Il s'agit donc d'un modèle qui
mêle régression à deux facteurs et analyse de
la variance à un facteur. On parle alors de modèle
d'analyse de la covariance. Les valeurs prises par les estimateurs
des moindres carrés, après application
numérique, sont :
Remarquons que pour chacun de ces coefficients on peut effectuer un
test de nullité, et ôter du modèle ceux qui ne
sont pas significativement différents de zéro. Il va
de soi que l'on préfère avoir le moins de
paramètres possible.
Ce modèle permet d'estimer les variations
saisonnières, et d'en déduire, par soustraction, la
série corrigée des variations saisonnières :
La qualité du modèle est évidente, tant les
valeurs prises par
 sont
proches de la série initiale. Cela est confirmé par
le coefficient de détermination
sont
proches de la série initiale. Cela est confirmé par
le coefficient de détermination 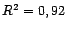 .
.
Section : Exemples
Précédent : Coefficient de détermination.
Suivant : Transport aérien
Thierry Cabanal-Duvillard
![\includegraphics[scale=.6]{Dessins/USAccDeaths03-1.epsi}](img148.gif)
![\includegraphics[scale=.6]{Dessins/USAccDeaths03-2.epsi}](img156.gif)
![]() , on fait
l'hypothèse d'un comportement parabolique. On est ainsi
ramené au modèle linéaire suivant
, on fait
l'hypothèse d'un comportement parabolique. On est ainsi
ramené au modèle linéaire suivant
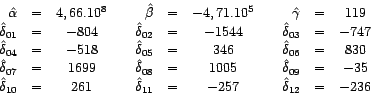
![\includegraphics[scale=.6]{Dessins/USAccDeaths03-3.epsi}](img160.gif)
![\includegraphics[scale=.6]{Dessins/USAccDeaths03-4.epsi}](img161.gif)
![\includegraphics[scale=.6]{Dessins/USAccDeaths03-5.epsi}](img163.gif)
![\includegraphics[scale=.6]{Dessins/USAccDeaths03-6.epsi}](img164.gif)
![]() sont
proches de la série initiale. Cela est confirmé par
le coefficient de détermination
sont
proches de la série initiale. Cela est confirmé par
le coefficient de détermination ![]() .
.