Section : Mortalité en Normandie
Précédent : Mortalité en Normandie
Suivant : Mortalité accidentelle
Un modèle linéaire décrit les variations
d'une série temporelle en distinguant celles qui sont dues
à la partie déterministe et qui sont
prévisibles et estimables, des fluctuations
imprévisibles du bruit blanc. Il sera d'autant plus
intéressant que la partie déterministe sera
prépondérante sur la partie aléatoire. Pour
évaluer cette pertinence du modèle, nous allons
introduire le coefficient de détermination.
Soient
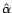 et
et
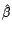 les estimateurs des moindres
carrés de
les estimateurs des moindres
carrés de 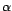 ,
, 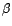 .
On note aussi
.
On note aussi
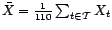 ,
,
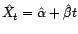 ,
,
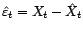 et
et
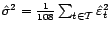 l'estimateur de
l'estimateur de
 . On a donc
. On a donc
La droite de régression
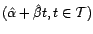 correspond à la valeur de la série à l'instant
correspond à la valeur de la série à l'instant
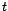 telle que le modèle permet de la
reconstruire, ce qu'on appelle la partie expliquée ; tandis
que le vecteur des résidus
telle que le modèle permet de la
reconstruire, ce qu'on appelle la partie expliquée ; tandis
que le vecteur des résidus
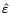 est la partie
inexpliquée, la part d'erreur résiduelle que le
modèle ne permet d'anticiper. Cette distinction se retrouve
en termes d'analyse de la variance, où l'on peut
séparer dans les variations de la série ce qui
revient aux variations de la partie expliquée de ce qui
ressort des variations de l'erreur résiduelle. On a en effet
l'équation
où
est la partie
inexpliquée, la part d'erreur résiduelle que le
modèle ne permet d'anticiper. Cette distinction se retrouve
en termes d'analyse de la variance, où l'on peut
séparer dans les variations de la série ce qui
revient aux variations de la partie expliquée de ce qui
ressort des variations de l'erreur résiduelle. On a en effet
l'équation
où
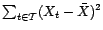 mesure la
variance totale de la série,
mesure la
variance totale de la série,
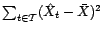 la
variance expliquée par le modèle, et
la
variance expliquée par le modèle, et
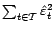 la
variance résiduelle.
la
variance résiduelle.
Il va de soi que l'on préfère avoir une variance
expliquée forte et une variance résiduelle faible. Le
coefficient de détermination
constitue comme une mesure de la qualité de la
régression, de la pertinence du modèle. Plus 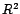 sera proche de 1, davantage les fluctuations de la
série seront expliquées par le modèle.
sera proche de 1, davantage les fluctuations de la
série seront expliquées par le modèle.
Dans le cas présent, l'application numérique donne
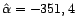 ,
,
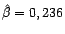 ,
,
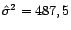 et
et 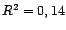 . Le modèle linéaire donne peu
d'information sur les variations de la série.
. Le modèle linéaire donne peu
d'information sur les variations de la série.
Section : Mortalité en Normandie
Précédent : Mortalité en Normandie
Suivant : Mortalité accidentelle
Thierry Cabanal-Duvillard
![]() et
et
![]() les estimateurs des moindres
carrés de
les estimateurs des moindres
carrés de ![]() ,
, ![]() .
On note aussi
.
On note aussi
![]() ,
,
![]() ,
,
![]() et
et
![]() l'estimateur de
l'estimateur de
![]() . On a donc
. On a donc
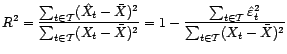
![]() ,
,
![]() ,
,
![]() et
et ![]() . Le modèle linéaire donne peu
d'information sur les variations de la série.
. Le modèle linéaire donne peu
d'information sur les variations de la série.![\includegraphics[scale=.6]{Dessins/Ger03-5.epsi}](img144.gif)
![\includegraphics[scale=.6]{Dessins/Ger03-6.epsi}](img145.gif)