Section : Transformation de Box-Cox
Précédent : Transformation de Box-Cox
Suivant : Exercice
3.
- Si la série
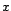 prend des valeurs
négatives ou nulles, il est loisible de lui rajouter
arbitrairement une constante afin d'obtenir une série
à termes positifs et avant d'effectuer une transformation de
Box-Cox.
prend des valeurs
négatives ou nulles, il est loisible de lui rajouter
arbitrairement une constante afin d'obtenir une série
à termes positifs et avant d'effectuer une transformation de
Box-Cox.
- Pour
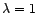 , la transformation de Box-Cox ne
modifie pas la série, en dehors d'une translation par 1 qui
n'a aucune incidence sur l'étude statistique.
, la transformation de Box-Cox ne
modifie pas la série, en dehors d'une translation par 1 qui
n'a aucune incidence sur l'étude statistique.
- Pour
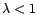 , l'effet de la transformation
de Box-Cox est de ramener à une amplitude constante des
variations qui croissent avec le niveau moyen de la tendance
générale. Plus
, l'effet de la transformation
de Box-Cox est de ramener à une amplitude constante des
variations qui croissent avec le niveau moyen de la tendance
générale. Plus 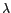 est proche
de 0, plus cet effet est important.
est proche
de 0, plus cet effet est important.
- Pour
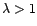 , l'effet est opposé,
et la transformation de Box-Cox est alors à utiliser avec
des séries dont les fluctuations croissent quand la
série elle-même décroît. C'est par
exemple le cas de la série associée au lac
Huron.
, l'effet est opposé,
et la transformation de Box-Cox est alors à utiliser avec
des séries dont les fluctuations croissent quand la
série elle-même décroît. C'est par
exemple le cas de la série associée au lac
Huron.
- Si l'amplitude des variations de la série est
négligeable devant son niveau moyen, alors l'effet d'une
transformation de Box-Cox peut se réduire à une
transformation affine, c'est-à-dire rester inutile. En
effet, si on note
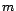 le niveau moyen de la
série, et si
le niveau moyen de la
série, et si
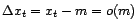 , alors
Pour remédier à cette inefficacité, il peut
être bon de soustraire une constante à la série
avant d'opérer la transformation de Box-Cox. On
modélisera alors la série
, alors
Pour remédier à cette inefficacité, il peut
être bon de soustraire une constante à la série
avant d'opérer la transformation de Box-Cox. On
modélisera alors la série
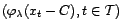 .
.
Le problème qui se pose est de choisir la valeur de 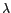 , voire de
, voire de 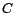 . Le choix de
. Le choix de 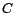 s'effectue en premier et est arbitraire. Quant au choix
de
s'effectue en premier et est arbitraire. Quant au choix
de 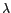 , il y a deux approches :
, il y a deux approches :
- Soit on se restreint à un petit nombre de valeurs
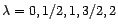 ; on essaie alors
celles qui sont le plus vraisemblable et on compare les
résultats.
; on essaie alors
celles qui sont le plus vraisemblable et on compare les
résultats.
- Soit on cherche à estimer la valeur de
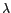 . Le modèle statistique est celui
associé à
. Le modèle statistique est celui
associé à
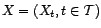 , vérifiant
avec
, vérifiant
avec 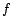 fonction linéaire de
fonction linéaire de
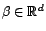 , et
, et
 bruit blanc de variance
bruit blanc de variance
 . On fait l'hypothèse que le
bruit blanc est gaussien. Le modèle est
paramètrisé par
. On fait l'hypothèse que le
bruit blanc est gaussien. Le modèle est
paramètrisé par
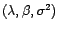 , et on
choisit alors l'estimateur de
, et on
choisit alors l'estimateur de 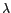 (puis de
(puis de
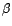 ) comme l'estimateur du maximum de
vraisemblance. Rappelons que dans le cas ordinaire où
) comme l'estimateur du maximum de
vraisemblance. Rappelons que dans le cas ordinaire où
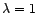 , l'estimateur des moindres
carrés de
, l'estimateur des moindres
carrés de 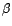 est l'estimateur du maximum
de vraisemblance du modèle gaussien.
est l'estimateur du maximum
de vraisemblance du modèle gaussien.
Section : Transformation de Box-Cox
Précédent : Transformation de Box-Cox
Suivant : Exercice
3.
Thierry Cabanal-Duvillard
![]() , voire de
, voire de ![]() . Le choix de
. Le choix de ![]() s'effectue en premier et est arbitraire. Quant au choix
de
s'effectue en premier et est arbitraire. Quant au choix
de ![]() , il y a deux approches :
, il y a deux approches :