Section : Modèles linéaires
Précédent : Lynx
Suivant : Remarques
Nous venons de voir l'intérêt de la fonction
logarithmique pour effectuer une transformation préalable
des données. On définit plus
généralement une famille de transformation, dite de
Box-Cox :
Si
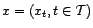 est une série
temporelle, opérer une transformation préalable de
Box-Cox conduit donc à modéliser la série
est une série
temporelle, opérer une transformation préalable de
Box-Cox conduit donc à modéliser la série
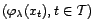 .
.
Sous-sections
Thierry Cabanal-Duvillard