On appelle moyenne mobile symétrique d'ordre ![]() la fonction qui à tout processus
la fonction qui à tout processus
![]() associe
le processus
associe
le processus
![]() avec
avec
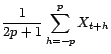 |
|||
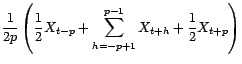
|
En choisissant ![]() puis
puis ![]() ,
voici les valeurs prises par la série
,
voici les valeurs prises par la série
![]() obtenue par le procédé de moyenne mobile :
obtenue par le procédé de moyenne mobile :
![\includegraphics[scale=.6]{Dessins/Huron03-3.epsi}](img75.gif)
![\includegraphics[scale=.6]{Dessins/Huron03-5.epsi}](img76.gif)
Au vu de cette estimation de ![]() , il
paraît peu justifié de faire l'hypothèse d'une
tendance affine. On supposera plutôt la tendance parabolique
, il
paraît peu justifié de faire l'hypothèse d'une
tendance affine. On supposera plutôt la tendance parabolique
![\includegraphics[scale=.6]{Dessins/Huron03-6.epsi}](img81.gif)
![\includegraphics[scale=.6]{Dessins/Huron03-7.epsi}](img82.gif)