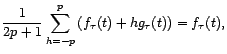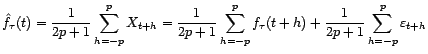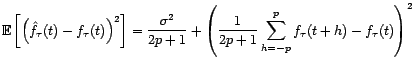Section : Exemples
Précédent : Exemples
Suivant : Notations
Le niveau du lac Huron, aux États-Unis, a
été mesuré pendant près d'un
siècle :
On n'observe pas de comportement saisonnier, seulement une
allure globalement décroissante. On suppose donc le
modèle de la forme
avec
 bruit blanc faible de variance
bruit blanc faible de variance
 , et
, et 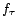 à déterminer.
à déterminer.
Pour une première estimation de la tendance, on utilise
un procédé de lissage à base de moyenne
mobile. A la base de cette technique, il y a l'idée que la
tendance est une fonction régulière du temps, et
qu'en tout point il est ``raisonnable'' de l'approximer par sa
tangente. Autrement dit, quel que soit
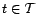 , il existe
, il existe
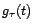 tel que
tel que
pour 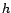 suffisamment petit. Si on remarque alors
que
on en déduit qu'on peut construire un estimateur raisonnable
de
suffisamment petit. Si on remarque alors
que
on en déduit qu'on peut construire un estimateur raisonnable
de
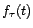 en faisant la moyenne des valeurs
prises par le processus
en faisant la moyenne des valeurs
prises par le processus  autour de
autour de 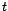 :
Le risque de cet estimateur vaut
Pour de faibles valeurs de
:
Le risque de cet estimateur vaut
Pour de faibles valeurs de  , le biais est
faible, mais la variance de l'estimateur est forte. Pour de plus
grandes valeurs de
, le biais est
faible, mais la variance de l'estimateur est forte. Pour de plus
grandes valeurs de  , la variance est moindre,
mais le biais peut devenir important. Il y a donc une valeur
optimale de
, la variance est moindre,
mais le biais peut devenir important. Il y a donc une valeur
optimale de  , qu'il est néanmoins difficile
de prévoir.
, qu'il est néanmoins difficile
de prévoir.
Sous-sections
Section : Exemples
Précédent : Exemples
Suivant : Notations
Thierry Cabanal-Duvillard
![\includegraphics[scale=.6]{Dessins/Huron03-1.epsi}](img49.gif)
![]() , il existe
, il existe
![]() tel que
tel que