Section : Conditionnement
Précédent : Conditionnement
Suivant : Exercices:
Soient  et
et 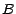 deux
événements d'un espace probabilisé
deux
événements d'un espace probabilisé
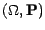 avec
avec
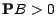 ; La probabilité
conditionnelle
; La probabilité
conditionnelle
![$ \textbf{P}[A\vert B]$](img246.gif) de
de  quand
quand 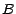 (on dit aussi "sachant
(on dit aussi "sachant 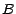 ") sera , par définition
") sera , par définition
On a évidemment les égalités
La fonction d'ensemble
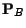 définie par
définie par
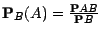 est donc
une nouvelle probabilité sur
est donc
une nouvelle probabilité sur  .
.
Les deux propriétés suivantes sont conformes à
l'idée intuitive que l'on se fait d'un conditionnement .
-
![$ \textbf{P}_B [B]=1$](img251.gif) ; (la probabilité
qu'il pleuve , sachant qu'il pleut , est égale à 1)
.
; (la probabilité
qu'il pleuve , sachant qu'il pleut , est égale à 1)
.
- Les événements invariants par ce changement de
probabilité sont exactement les événements
indépendants de
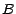 ; (la probabilité de
; (la probabilité de
 : il va pleuvoir est modifiée
par la connaissance de l'événement : le temps est
couvert , mais ne l'est pas par celle de
l'événement indépendant : j'ai un brelan
servi) .
: il va pleuvoir est modifiée
par la connaissance de l'événement : le temps est
couvert , mais ne l'est pas par celle de
l'événement indépendant : j'ai un brelan
servi) .
Sous-sections
Jacques Azéma
![]() et
et ![]() deux
événements d'un espace probabilisé
deux
événements d'un espace probabilisé
![]() avec
avec
![]() ; La probabilité
conditionnelle
; La probabilité
conditionnelle
![]() de
de ![]() quand
quand ![]() (on dit aussi "sachant
(on dit aussi "sachant ![]() ") sera , par définition
") sera , par définition