Section : Conditionnement par un événement
Précédent : Exercice : Conditionnement d'une
Suivant : Exemples:
Soient  une variable aléatoire réelle
et
une variable aléatoire réelle
et 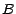 un événement de
probabilité non nulle ; l' espérance de
un événement de
probabilité non nulle ; l' espérance de  relativement à la probabilité
relativement à la probabilité
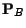 (introduite au début de
ce chapitre) , sera notée
(introduite au début de
ce chapitre) , sera notée
![$ \textbf{E}_B[X]$](img282.gif) ou
ou
![$ \textbf{E}[X\vert B]$](img283.gif) et sera appelée
espérance conditionnelle de
et sera appelée
espérance conditionnelle de  quand
quand 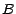 . L'égalité
. L'égalité
![$\displaystyle \textbf{E}[X\vert B] =\frac{\textbf{E}[X1_B]}{\textbf{P}B}$](img284.gif)
|
(2.3) |
se démontre aisément si l'on a retenu (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) dont nous
reprenons les notations ; on a en effet
Le calcul pratique de l'espérance conditionnelle d'une
variable aléatoire s'effectue à l'aide de sa loi
conditionnelle ; appliquant (
) dont nous
reprenons les notations ; on a en effet
Le calcul pratique de l'espérance conditionnelle d'une
variable aléatoire s'effectue à l'aide de sa loi
conditionnelle ; appliquant (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) à la
probabilité
) à la
probabilité
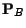 , on obtient en effet
, on obtient en effet
![$\displaystyle \textbf{E}[X\vert B]=\sum_{k\in X(\Omega)}k\Pi_{X/B}(k)$](img286.gif)
|
(2.4) |
Sous-sections
Jacques Azéma
![$\displaystyle \textbf{E}[X\vert B] =\frac{\textbf{E}[X1_B]}{\textbf{P}B}$](img284.gif)
![$\displaystyle \textbf{E}[X\vert B] =\frac{\textbf{E}[X1_B]}{\textbf{P}B}$](img284.gif)