Section : Les
indicateurs
Précédent : Les indicateurs
Suivant : Espérance d'une variable aléatoire
- Soient
 une v.a. à valeurs dans
une v.a. à valeurs dans  et
et 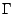 un sous ensemble de
un sous ensemble de  ; on a l'égalité
; on a l'égalité
![$\displaystyle 1_{[X\in\Gamma]}=1_\Gamma\circ X$](img75.gif) |
(1.3) |
Ainsi , dans l'exemple 1.2.2 b) , définissons les
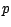 indicateurs
indicateurs
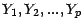 par
par
![$ Y_i=1_{[X_i\in E_1]}=1_{E_1}\circ X_i\;\; ;$](img77.gif) on a alors l'égalité
on a alors l'égalité
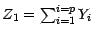 .
.
- Soit
 une v.a. réelle ; on note (
une v.a. réelle ; on note (
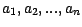 ) une
énumération de
) une
énumération de  où
les
où
les 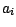 sont distincts et
sont distincts et 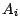 l'événement
l'événement ![$ [X=a_i]$](img82.gif) . La suite
(
. La suite
(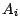 ) constitue une partition de
) constitue une partition de  et l'on peut écrire
et l'on peut écrire
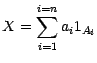 |
(1.4) |
La démonstration de ces 2 points est immédiate : il
suffit de vérifier que les fonctions figurant aux 2 membres
de (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) et de (
) et de (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) prennent la
même valeur en tout point
) prennent la
même valeur en tout point  . Nous
invitons le lecteur inexpérimenté à prendre
quelques minutes pour écrire la démonstration
complète de manière à s'assurer qu'il a
assimilé les définitions et notations du début
de ce cours .
. Nous
invitons le lecteur inexpérimenté à prendre
quelques minutes pour écrire la démonstration
complète de manière à s'assurer qu'il a
assimilé les définitions et notations du début
de ce cours .
Section : Les
indicateurs
Précédent : Les indicateurs
Suivant : Espérance d'une variable aléatoire
Jacques Azéma