Section : Les
variables aléatoires et
Précédent : Retour aux exemples
Suivant : Deux
propriétés à retenir
Soient  un ensemble et
un ensemble et 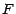 un sous
ensemble de
un sous
ensemble de  ; l'indicateur de
; l'indicateur de 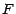 sera par définition la fonction
sera par définition la fonction
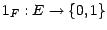 définie par
définie par
Sur un espace de probabilité , l'indicateur d'un
événement  est donc une variable
aléatoire á valeursdans
est donc une variable
aléatoire á valeursdans 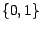 ;
leur utilisation permet de remplacer les opérations
booléennes sur les ensembles (intersection , réunion
etc ...) par des calculs algébriques ordinaires . Par
exemple ,
Cela justifie les notations
;
leur utilisation permet de remplacer les opérations
booléennes sur les ensembles (intersection , réunion
etc ...) par des calculs algébriques ordinaires . Par
exemple ,
Cela justifie les notations
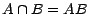 et
et
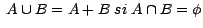 .
.
Sous-sections
Jacques Azéma
![]() un ensemble et
un ensemble et ![]() un sous
ensemble de
un sous
ensemble de ![]() ; l'indicateur de
; l'indicateur de ![]() sera par définition la fonction
sera par définition la fonction
![]() définie par
définie par