Section : Loi d'une
variable aléatoire
Précédent : Loi d'une variable aléatoire
Suivant : Exercices
Soient  une v.a. à valeurs dans
une v.a. à valeurs dans  et
et  une application de
une application de  dans
dans
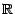 ;
; 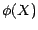 est
alors une variable aléatoire réelle dont
l'espérance est donnée par la formule :
est
alors une variable aléatoire réelle dont
l'espérance est donnée par la formule :
![$\displaystyle \textbf{E}[\phi (X)] = \sum_{k\in X(\Omega)}\phi (k)\Pi_X(k) .$](img130.gif)
|
(1.7) |
Démonstration : Ce résultat découle
immédiatement de l'égalité (à peu
près évidente , si l'on a réfléchi
à (![[*]](file:/usr/share/latex2html/icons/crossref.gif) )
)
et de la linéarité de l'espérance
)
)
et de la linéarité de l'espérance
Dans le cas où  est elle réelle , on
a en particulier
est elle réelle , on
a en particulier
![$\displaystyle \textbf{E}[X]=\sum_{k\in X(\Omega)}k\Pi_X(k) \;\;\; , \;\;\;\text... ... X(\Omega)}k^r\Pi_X(k)\;\;,\;\;\textbf{E}[s^X]=\sum_{k\in X(\Omega)}s^k\Pi_X(k)$](img132.gif)
|
(1.8) |
Par exemple , si  suit une loi binomiale de
paramètres
suit une loi binomiale de
paramètres
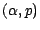 , on a
Le calcul du second membre est un exercice classique sur la formule
du binôme (développer
, on a
Le calcul du second membre est un exercice classique sur la formule
du binôme (développer 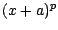 ,
dériver , puis faire
,
dériver , puis faire 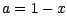 dans
l'égalité obtenue) ; on obtient
dans
l'égalité obtenue) ; on obtient
![$ \textbf{E}[X]= p \alpha $](img137.gif) ; on retrouve ainsi
d'une autre façon la valeur trouvée en 1.2.4
pour l'espérance de
; on retrouve ainsi
d'une autre façon la valeur trouvée en 1.2.4
pour l'espérance de 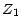 (dans ce cas ,
(dans ce cas ,
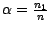 )
)
Jacques Azéma
![$\displaystyle \textbf{E}[\phi (X)] = \sum_{k\in X(\Omega)}\phi (k)\Pi_X(k) .$](img130.gif)
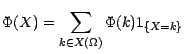
![$\displaystyle \textbf{E}[X]=\sum_{k\in X(\Omega)}k\Pi_X(k) \;\;\; , \;\;\;\text... ... X(\Omega)}k^r\Pi_X(k)\;\;,\;\;\textbf{E}[s^X]=\sum_{k\in X(\Omega)}s^k\Pi_X(k)$](img132.gif)
![$\displaystyle \textbf{E}[X]=\sum_{k=0}^{k=p}k \left( \begin{array}{c} p\\ k \end{array}\right) \alpha ^k(1-\alpha )^{p-k} .$](img134.gif)