Section : Loi d'une
variable aléatoire
Précédent : Proposition:
Suivant : Loi d'un
couple de
- Calculer , dans le même esprit , le moment d'ordre 2 et
la variance de
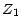
- Dans l'exemple d) , montrer que
![$ \textbf{E}[\;\sharp (F\cap G)]={pq\over n}$](img139.gif) .
.
Indications: Il s'agit de calculer (Cf (![[*]](file:/usr/share/latex2html/icons/crossref.gif) )) ,
)) ,
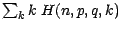 ; après avoir
montré l'identité
; après avoir
montré l'identité
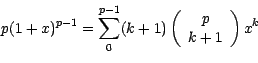 , on identifiera les termes en
, on identifiera les termes en 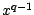 dans
l'égalité entre polynômes
dans
l'égalité entre polynômes
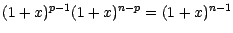
Jacques Azéma
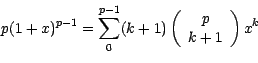 , on identifiera les termes en
, on identifiera les termes en 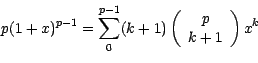 , on identifiera les termes en
, on identifiera les termes en