Section : Les
variables aléatoires et
Précédent : Exercices
Suivant : Exercice
Soient
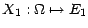 et
et
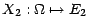 deux variables
aléatoires définies sur le même espace de
probabilité
deux variables
aléatoires définies sur le même espace de
probabilité
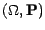 .
.
Posons , pour tout
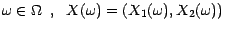 ;
;  est alors une variable aléatoire
à valeurs dans l'espace produit
est alors une variable aléatoire
à valeurs dans l'espace produit
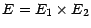 , que l'on appellera le
couple
, que l'on appellera le
couple 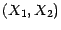 . Posons
. Posons
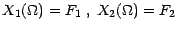 ; on
peut appliquer les définitions et les résultats du
paragraphe précédent à la variable
aléatoire
; on
peut appliquer les définitions et les résultats du
paragraphe précédent à la variable
aléatoire  ; il en résulte que:
; il en résulte que:
- La loi
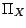 du couple
du couple 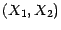 est une probabilité sur l'ensemble fini
est une probabilité sur l'ensemble fini
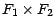
- Soit
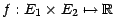 ;
;
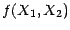 est alors une variable
aléatoire réelle et
avec les cas particuliers suivants , obtenus en choisissant
convenablement la fontion
est alors une variable
aléatoire réelle et
avec les cas particuliers suivants , obtenus en choisissant
convenablement la fontion 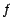 ,
,
- Si
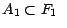 ,
,
- Soit
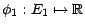 ; on a
; on a
Les loi de chacune des deux variables
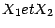 sont appelées lois
marginales du couple ; il resulte des 2 points qui
précèdent qu'on les déduit aisément de
la loi
sont appelées lois
marginales du couple ; il resulte des 2 points qui
précèdent qu'on les déduit aisément de
la loi 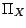 ; par exemple ,
Inversement , on ne peut pas déduire la loi d'un couple
de la seule connaissance de ses lois marginales.
; par exemple ,
Inversement , on ne peut pas déduire la loi d'un couple
de la seule connaissance de ses lois marginales.
Pour s'en convaincre , on réfléchira à
l'exercice suivant :
Sous-sections
Section : Les
variables aléatoires et
Précédent : Exercices
Suivant : Exercice
Jacques Azéma
![]() et
et
![]() deux variables
aléatoires définies sur le même espace de
probabilité
deux variables
aléatoires définies sur le même espace de
probabilité
![]() .
.![]() ;
; ![]() est alors une variable aléatoire
à valeurs dans l'espace produit
est alors une variable aléatoire
à valeurs dans l'espace produit
![]() , que l'on appellera le
couple
, que l'on appellera le
couple ![]() . Posons
. Posons![]() ; on
peut appliquer les définitions et les résultats du
paragraphe précédent à la variable
aléatoire
; on
peut appliquer les définitions et les résultats du
paragraphe précédent à la variable
aléatoire ![]() ; il en résulte que:
; il en résulte que:![$\displaystyle \textbf{E}[f(X_1,X_2)]=\sum_{x_1\in F_1;x_2\in F_2} f(x_1,x_2) \Pi_X(x_1,x_2)$](img153.gif)
![$\displaystyle \;\; \textbf{P}[X_1\in A_1] = \Pi_{X_1}A_1=\Pi_X(A_1\times F_2) = \sum_{x_1\in A_1;x_2\in F_2}\Pi _X(x_1,x_2)$](img156.gif)
![$\displaystyle \textbf{E}[\phi _1 (X_1)] = \sum_{x_1\in F_1;x_2\in F_2}\phi _1(x_1) \Pi _X(x_1,x_2)$](img158.gif)