Section : Exercice
Précédent : La notion de de
Suivant : Indépendance
Sans le dire , nous avons supposé que notre sondage
préélectoral concernait le second tour des
élections présidentielles (il ne restait que 2
candidats) ; on peut, sans changer d'espace de probabilité,
revenir 15 jours en arrière et s'intéresser au
premier tour , à ses 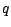 candidats ,et
surtout à leurs électeurs qui forment une partition
candidats ,et
surtout à leurs électeurs qui forment une partition
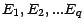 de la population
de la population  ; on posera
; on posera
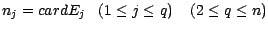 et
l'on se rappellera que
et
l'on se rappellera que
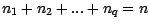 . On pose ensuite
(
. On pose ensuite
(
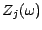 représente le nombre
d'électeurs du candidat
représente le nombre
d'électeurs du candidat 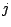 figurant sur la
liste
figurant sur la
liste 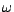 de
de 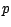 électeurs
ramenée par notre enquêteur) . Notons au passage que
électeurs
ramenée par notre enquêteur) . Notons au passage que
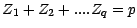 , et posons
, et posons
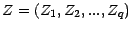 .
.
Le calcul des lois marginales de 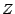 est facile et sera
laissé au lecteur ( la loi de
est facile et sera
laissé au lecteur ( la loi de 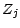 , est
binomiale de paramètres (
, est
binomiale de paramètres (
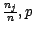 )) ; intéressons nous
maintenant à la loi de
)) ; intéressons nous
maintenant à la loi de 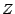 , c'est à
dire aux quantités
, c'est à
dire aux quantités
quand
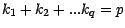 .
.
Nous avons donc à calculer le cardinal 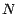 de l'ensemble des suites de taille
de l'ensemble des suites de taille 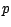 qui ont
qui ont 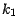 termes dans
termes dans 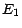 ,
,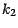 termes dans
termes dans 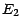 etc...Pour faire cela , on
remarque d'abord que le nombre de suites dont les
etc...Pour faire cela , on
remarque d'abord que le nombre de suites dont les 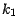 premiers termes sont dans
premiers termes sont dans 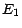 , les
, les
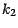 suivants dans
suivants dans 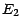 ,...,et les
,...,et les 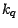 derniers dans
derniers dans 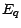 est égal à
est égal à
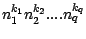 ;
; 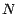 s'obtient en multipliant cette quantité par le
nombre
s'obtient en multipliant cette quantité par le
nombre 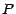 de partitions de
de partitions de
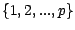 en sous ensembles de
cardinaux
en sous ensembles de
cardinaux
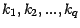 ; Or ,
; Or , 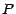 est égal à
On obient donc finalement:
Cette loi de probabilité sur
est égal à
On obient donc finalement:
Cette loi de probabilité sur
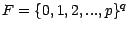 est appelée loi
multinomiale de paramètres
est appelée loi
multinomiale de paramètres
(
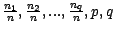 ) . On
remarquera que son support est le sous ensemble strict de
) . On
remarquera que son support est le sous ensemble strict de 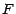 :
:
Section : Exercice
Précédent : La notion de de
Suivant : Indépendance
Jacques Azéma