Section : Conditionnement par un événement
Précédent : Exercice :
Suivant : Exercice
:
Soient
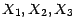 trois v.a.r.
indépendantes ,
trois v.a.r.
indépendantes ,
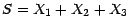 ; on appelle
; on appelle 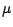 la loi de
la loi de 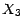 ; montrer que la loi
conditionnelle de
; montrer que la loi
conditionnelle de 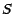 quand
quand
![$ [X_1=i;X_2=j]$](img303.gif) est donnée par
est donnée par
![$\displaystyle \textbf{P}[S=k\;\vert\;X_1=i\; ; X_2=j]=\mu (k-i-j) ;$](img304.gif)
|
(2.9) |
en déduire l'égalité
![$\displaystyle \textbf{E}[S\;\vert\;X_1=i\;;\;X_2=j]=i+j+\textbf{E}[X_3] .$](img305.gif)
|
(2.10) |
Montrer (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) directement
(i.e. sans calculer la loi conditionnelle de
) directement
(i.e. sans calculer la loi conditionnelle de 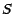 )
.
)
.
Jacques Azéma