Section : Conditionnement par un événement
Précédent : Exercice :
Suivant : Exercice
:
On dira que  est indépendante de
est indépendante de 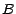 si les v.a.
si les v.a.  et
et 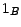 sont
indépendantes ; pour qu'il en soit ainsi, il faut et il
suffit que
sont
indépendantes ; pour qu'il en soit ainsi, il faut et il
suffit que ![$ [X=k]$](img291.gif) soit indépendant de
soit indépendant de
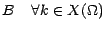 ce qui
s'écrit encore
ce qui
s'écrit encore
L'égalité
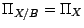 |
(2.6) |
est donc une condition nécessaire et suffisante assurant
l'indépendance de  et
et 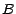 . On
notera que (
. On
notera que (![[*]](file:/usr/share/latex2html/icons/crossref.gif) )
entraîne
)
entraîne
![$\displaystyle \textbf{E}[X\vert B]=\textbf{E}[X]$](img295.gif) |
(2.7) |
Jacques Azéma
![]() est indépendante de
est indépendante de ![]() si les v.a.
si les v.a. ![]() et
et ![]() sont
indépendantes ; pour qu'il en soit ainsi, il faut et il
suffit que
sont
indépendantes ; pour qu'il en soit ainsi, il faut et il
suffit que ![]() soit indépendant de
soit indépendant de
![]() ce qui
s'écrit encore
ce qui
s'écrit encore