Section : Loi
conditionnelle d'une variable
Précédent : Loi conditionnelle d'une variable
Suivant : Exercice
: Conditionnement d'une
On joue  fois à un jeu de pile ou face
biaisé ; le
fois à un jeu de pile ou face
biaisé ; le
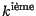 coup est
représenté par une v.a.
coup est
représenté par une v.a. 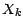 de
Bernoulli vérifiant
de
Bernoulli vérifiant
![$ \textbf{P}[X_k =1] =\alpha$](img258.gif) ; la suite de
v.a. (
; la suite de
v.a. (
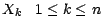 ) est supposée
indépendante. Si
) est supposée
indépendante. Si 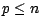 ,
,
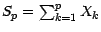 représente le
nombre de piles tombés au cours des
représente le
nombre de piles tombés au cours des 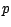 premiers
coups ; nous savons que la loi de
premiers
coups ; nous savons que la loi de 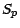 est
binomiale de paramètres
est
binomiale de paramètres
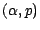 .
.
Donnons nous maintenant un autre entier 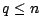 et
examinons la loi de
et
examinons la loi de 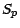 quand
quand ![$ [S_n=q]$](img264.gif) . On a
La dernière égalité provenant de ce que
. On a
La dernière égalité provenant de ce que 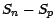 est indépendante de
est indépendante de 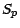 et a même loi que
et a même loi que 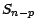 . Un
calcul facile montre alors que
. Un
calcul facile montre alors que
![$\displaystyle \textbf{P}[S_p=k\;\vert\;S_n=q]=\frac{ \left( \begin{array}{c} p\... ... n\\ q \end{array} \right)}\;\;\;\;\;\;\;\;\;\;((p+q-n)_+\leq k\leq p \wedge q)$](img268.gif)
|
(2.1) |
En particulier , pour 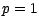 ,
,
![$\displaystyle \textbf{P}[X_1=1\;\vert\;S_n=q]=\textbf{P}[S_1=1\;\vert\;S_n=q]={q\over n}\;\;\;,\;\;\;\textbf{P}[X_1=0\;\vert\;S_n=q]=1-{q\over n}$](img270.gif)
|
(2.2) |
Dans le conditionnement par l'événement ![$ [S_n=q]$](img264.gif) la loi binomiale de
la loi binomiale de 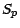 est
devenue la loi hypergéométrique rencontrée au
paragraphe (1.2.5.) ; celle de
est
devenue la loi hypergéométrique rencontrée au
paragraphe (1.2.5.) ; celle de 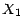 est quant
à elle restée une loi de Bernoulli mais avec un
paramètre différent . On remarquera que les lois
conditionnelles trouvées ne dépendent plus de
est quant
à elle restée une loi de Bernoulli mais avec un
paramètre différent . On remarquera que les lois
conditionnelles trouvées ne dépendent plus de 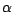
Section : Loi
conditionnelle d'une variable
Précédent : Loi conditionnelle d'une variable
Suivant : Exercice
: Conditionnement d'une
Jacques Azéma
![$\displaystyle \textbf{P}[S_p=k \;\vert\;S_n=q] = \frac{\textbf{P}[S_p=k\; ;S_n=... ...f{P}[S_n=q]}=\frac{\textbf{P}[S_p=k]\textbf{P}[S_{n-p}=q-k]}{\textbf{P}[S_n=q]}$](img265.gif)
![$\displaystyle \textbf{P}[S_p=k \;\vert\;S_n=q] = \frac{\textbf{P}[S_p=k\; ;S_n=... ...f{P}[S_n=q]}=\frac{\textbf{P}[S_p=k]\textbf{P}[S_{n-p}=q-k]}{\textbf{P}[S_n=q]}$](img265.gif)