Section : Estimation des caractéristiques d'un
Précédent : Exercice 1.
Suivant : Remarque.
Si  est un processus faiblement stationnaire
centré et régulier, sa décomposition de Wold
s'écrit
est un processus faiblement stationnaire
centré et régulier, sa décomposition de Wold
s'écrit
avec
 bruit blanc d'innovation. Les
paramètres de cette décomposition sont les
coefficients
bruit blanc d'innovation. Les
paramètres de cette décomposition sont les
coefficients
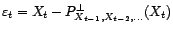 et la variance
et la variance
 de
de
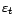 . Pour les déterminer,
il semble naturel de calculer
. Pour les déterminer,
il semble naturel de calculer
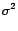 , et
d'en déduire
, et
d'en déduire
Or on ne peut calculer
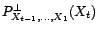 , mais
seulement les approximations
, mais
seulement les approximations
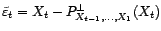 (grâce aux équations de Yule-Walker par exemple).
Notons
(grâce aux équations de Yule-Walker par exemple).
Notons
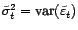 et
et
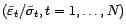 . La famille
. La famille
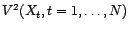 n'est autre que la base orthonormée de
n'est autre que la base orthonormée de
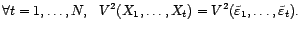 construite par le
procédé de Schmidt. En particulier, on a la
propriété :
C'est l'analogue fini-dimensionnel de la propriété
classique vérifiée par le bruit blanc d'innovation
d'un processus ARMA (ou d'un processus faiblement stationnaire
régulier) :
Posons pour tout
construite par le
procédé de Schmidt. En particulier, on a la
propriété :
C'est l'analogue fini-dimensionnel de la propriété
classique vérifiée par le bruit blanc d'innovation
d'un processus ARMA (ou d'un processus faiblement stationnaire
régulier) :
Posons pour tout
 alors
alors
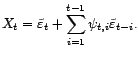 , et
Rappelons que dans le cas d'un processus ARMA (ou d'un processus
faiblement stationnaire régulier), de bruit blanc
d'innovation
, et
Rappelons que dans le cas d'un processus ARMA (ou d'un processus
faiblement stationnaire régulier), de bruit blanc
d'innovation
 , on a
avec
, on a
avec
Sous-sections
Section : Estimation des caractéristiques d'un
Précédent : Exercice 1.
Suivant : Remarque.
Thierry Cabanal-Duvillard
![]() est un processus faiblement stationnaire
centré et régulier, sa décomposition de Wold
s'écrit
est un processus faiblement stationnaire
centré et régulier, sa décomposition de Wold
s'écrit
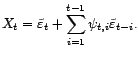 , et
, et