Section : Autocovariance et autocorrélation
empiriques
Précédent : Remarque :
Suivant : Algorithme des innovations
1) Soit
 un processus
stationnaire vérifiant
avec
un processus
stationnaire vérifiant
avec
 bruit blanc. Déterminer
sa fonction d'autocorrélation. (On pourra établir une
relation de récurrence entre
bruit blanc. Déterminer
sa fonction d'autocorrélation. (On pourra établir une
relation de récurrence entre
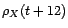 et
et
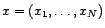 , et la résoudre.)
, et la résoudre.)
2) Soit
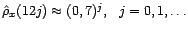 une série
temporelle dont la fonction d'autocorrélation estimée
a l'allure suivante :
une série
temporelle dont la fonction d'autocorrélation estimée
a l'allure suivante :
Proposer, en le justifiant, un modèle ARMA(12,1), pour
cette série.
Thierry Cabanal-Duvillard
![]() une série
temporelle dont la fonction d'autocorrélation estimée
a l'allure suivante :
une série
temporelle dont la fonction d'autocorrélation estimée
a l'allure suivante :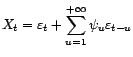 sinon.
sinon.