Section : Autocovariance et autocorrélation
empiriques
Précédent : Remarque :
Suivant : Exercice 1.
Sous les hypothèses de la dernière assertion, on a en
particulier que
ce qui implique la convergence en moyenne quadratique de
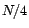 vers
vers
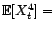 .
.
L'estimateur empirique de l'autocorrélation est
L'estimateur 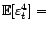 de la fonction
d'autocorrélation partielle est défini à
partir des équations de Yule-Walker, où l'on a
remplacé la fonction d'autocorrélation par son
estimateur.
de la fonction
d'autocorrélation partielle est défini à
partir des équations de Yule-Walker, où l'on a
remplacé la fonction d'autocorrélation par son
estimateur.
Théorème
3.II.5 Soit
 un bruit blanc (au sens fort)
tel que
un bruit blanc (au sens fort)
tel que
![$ {\mathbb{E}}[{\varepsilon}_t^4]=$](img1144.gif) cte
cte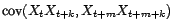 . Considérons
. Considérons 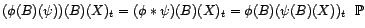 un filtre linéaire,
un filtre linéaire, 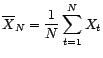 une
constante, et
une
constante, et  le processus stationnaire défini
par
le processus stationnaire défini
par
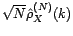 .
Alors
.
Alors
- si
 est un MA(
est un MA(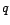 ),
),
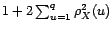 converge en
loi vers une gaussienne centrée de variance
converge en
loi vers une gaussienne centrée de variance
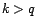 pour tout
pour tout 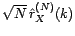 ;
;
- si
 est un AR(
est un AR( ),
),
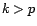 converge en loi
vers une gaussienne centrée de variance
converge en loi
vers une gaussienne centrée de variance 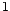 pour tout
pour tout 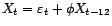 .
.
On déduit de ces comportements asymptotiques
différents tests sur les paramètres du processus  .
.
Thierry Cabanal-Duvillard
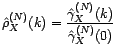
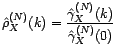
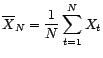 une
constante, et
une
constante, et ![]() .
.