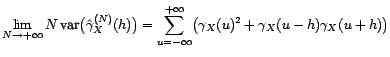Section : Autocovariance et autocorrélation
empiriques
Précédent : Démonstration du théorème
Suivant : Remarque :
Si la moyenne 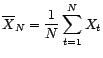 du processus
du processus  est connue - en particulier si le processus est
centré -, alors on définit plutôt
est connue - en particulier si le processus est
centré -, alors on définit plutôt
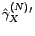 et
et
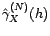 par
par
Dans ce cas,
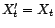 est un
estimateur sans biais de
est un
estimateur sans biais de
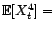 .
.
Théorème 3.II.4 Soit  un processus faiblement stationnaire tel que
un processus faiblement stationnaire tel que
-
![$ {\mathbb{E}}[X_t^4]=$](img1133.gif) cte
cte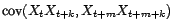 ;
;
-
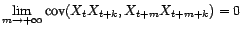 est indépendant de
est indépendant de 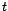 ;
;
-
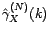 ;
;
alors
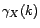 converge au sens
hilbertien vers
converge au sens
hilbertien vers
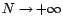 quand
quand
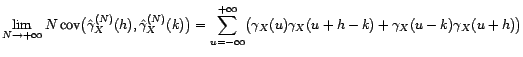 . Si, en outre,
. Si, en outre,  est un processus gaussien, et si
est un processus gaussien, et si
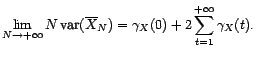 , alors
, alors
Thierry Cabanal-Duvillard
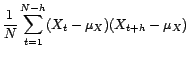
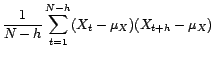
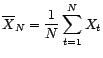 du processus
du processus 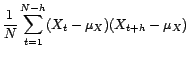
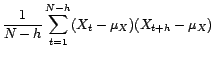
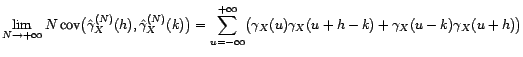 . Si, en outre,
. Si, en outre, 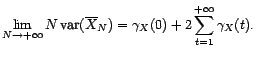 , alors
, alors