Section : Autocovariance et autocorrélation
empiriques
Précédent : Autocovariance et autocorrélation
empiriques
Suivant : Remarque :
Pour montrer le point ![[*]](file:/usr/share/latex2html/icons/crossref.gif) ,
définissons, pour tout
,
définissons, pour tout
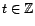 ,
, 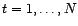 si
si
 , et
, et
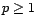 sinon. Soient
sinon. Soient 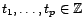 ,
,
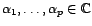 et
et
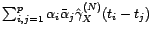 quelconques ; il s'agit de montrer que
quelconques ; il s'agit de montrer que
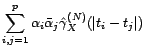 est positif :
est positif :
Le point ![[*]](file:/usr/share/latex2html/icons/crossref.gif) est également purement calculatoire, et ne
présente pas de mystère ; pour simplifier les
formules, supposons simplement que
est également purement calculatoire, et ne
présente pas de mystère ; pour simplifier les
formules, supposons simplement que  est
centré :
est
centré :
On en déduit le résultat car
![$ N{\mathbb{E}}[\bar X_N^2]=N\mathop{\hbox{\upshape {var}}}\nolimits (\bar X_N)$](img1124.gif) tend vers
tend vers
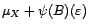 , et que le
dernier terme est une somme finie, bornée,
d'espérances qui tendent toutes vers 0 car
, et que le
dernier terme est une somme finie, bornée,
d'espérances qui tendent toutes vers 0 car
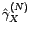 tend vers
0.
tend vers
0.
Section : Autocovariance et autocorrélation
empiriques
Précédent : Autocovariance et autocorrélation
empiriques
Suivant : Remarque :
Thierry Cabanal-Duvillard
![]() ,
définissons, pour tout
,
définissons, pour tout
![]() ,
, ![]() si
si
![]() , et
, et
![]() sinon. Soient
sinon. Soient ![]() ,
,
![]() et
et
![]() quelconques ; il s'agit de montrer que
quelconques ; il s'agit de montrer que
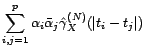 est positif :
est positif :
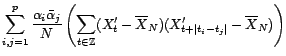
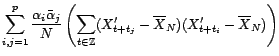
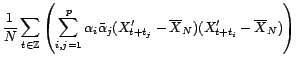
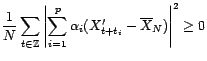
![$\displaystyle N{\mathbb{E}}\left[\hat{\gamma}_X^{(N)}(h)-{\gamma}_X(h)\right]$](img1119.gif)
![$\displaystyle (N-h){\gamma}_X(h)-N{\mathbb{E}}[\bar X_N^2]$](img1121.gif)
![$\displaystyle +\sum_{t=N-h+1}^N{\mathbb{E}}[\bar X_NX_t]-N{\mathbb{E}}[\bar X_N... ...m_{t=1}^h{\mathbb{E}}[\bar X_NX_t]+(N-h){\mathbb{E}}[\bar X_N^2]-N{\gamma}_X(h)$](img1122.gif)