Section : Estimation des caractéristiques d'un
Précédent : Démonstration du corollaire
Suivant : Démonstration du théorème
Plusieurs estimateurs empiriques peuvent être
définis pour l'autocovariance d'un processus  faiblement stationnaire. Le plus usuel est
faiblement stationnaire. Le plus usuel est
En pratique, on évite de calculer
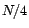 pour des valeurs de
pour des valeurs de
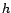 supérieures à
supérieures à 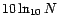 (certains préconisent plutôt
(certains préconisent plutôt
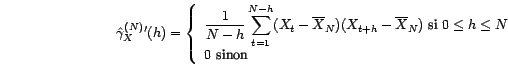 ).
).
On définit une variante de cet estimateur par
Théorème
3.II.3 Soit  un processus
faiblement stationnaire.
un processus
faiblement stationnaire.
-
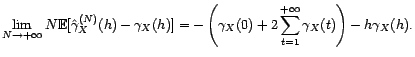 est de
type positif.
est de
type positif.
- Si de plus
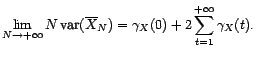 , alors
Même résultat pour
, alors
Même résultat pour
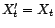 .
.
Sous-sections
Thierry Cabanal-Duvillard
![]() faiblement stationnaire. Le plus usuel est
faiblement stationnaire. Le plus usuel est
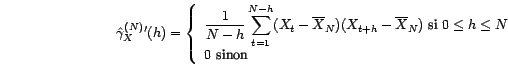 ).
).