Section : Estimation de la moyenne
Précédent : Démonstration du théorème
Suivant : Autocovariance et autocorrélation
empiriques
dans le cas où
 est un bruit blanc gaussien.
Tout processus
est un bruit blanc gaussien.
Tout processus  de la forme
de la forme
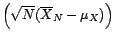 vérifie l'hypothèse
vérifie l'hypothèse
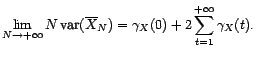 . Il résulte alors du théorème
. Il résulte alors du théorème ![[*]](file:/usr/share/latex2html/icons/crossref.gif) que
que
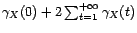 est une
gaussienne centrée dont la variance converge quand
est une
gaussienne centrée dont la variance converge quand 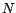 tend vers l'infini. Un résultat très
classique nous permet d'en conclure que la suite de gaussiennes
tend vers l'infini. Un résultat très
classique nous permet d'en conclure que la suite de gaussiennes
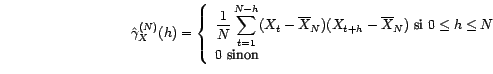 converge en loi
quand
converge en loi
quand 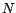 tend vers l'infini, vers une gaussienne
centrée de variance la limite des variances (il suffit, pour
s'en convaincre, d'étudier la convergence des fonctions
caractéristiques).
tend vers l'infini, vers une gaussienne
centrée de variance la limite des variances (il suffit, pour
s'en convaincre, d'étudier la convergence des fonctions
caractéristiques).
Les résultats précédents permettent de
construire des statistiques de tests asymptotiques, pour tester si
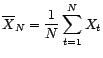 est nul ou non.
est nul ou non.
Thierry Cabanal-Duvillard
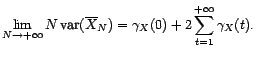 . Il résulte alors du théorème
. Il résulte alors du théorème 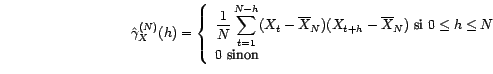 converge en loi
quand
converge en loi
quand 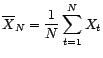 est nul ou non.
est nul ou non.