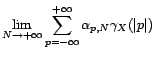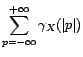Section : Estimation de la moyenne
Précédent : Estimation de la moyenne
Suivant : Démonstration du corollaire
Le point ![[*]](file:/usr/share/latex2html/icons/crossref.gif) est évident. Le second est une conséquence de
l'égalité suivante :
est évident. Le second est une conséquence de
l'égalité suivante :
Or un résultat classique sur les moyennes de Césaro
nous apprend que si
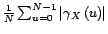 tend
vers 0 quand
tend
vers 0 quand 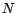 tend vers l'infini, alors
tend vers l'infini, alors
 converge aussi vers 0. Cela achève de démontrer le
point
converge aussi vers 0. Cela achève de démontrer le
point ![[*]](file:/usr/share/latex2html/icons/crossref.gif) .
Montrons le point
.
Montrons le point ![[*]](file:/usr/share/latex2html/icons/crossref.gif) : on a
avec
: on a
avec
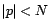 si
si
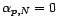 et
et
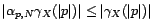 sinon. Pour tout
sinon. Pour tout 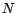 , on a
, on a
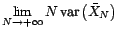 et
et
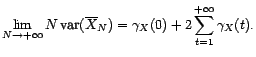 . On peut donc appliquer le théorème de convergence
dominée, et en déduire
. On peut donc appliquer le théorème de convergence
dominée, et en déduire
Corollaire 3.II.2
Théorème central limite. Soit 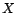 un processus fortement stationnaire vérifiant
avec
un processus fortement stationnaire vérifiant
avec
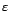 bruit blanc fort de variance
bruit blanc fort de variance
 et
et 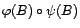 filtre linéaire. Alors
filtre linéaire. Alors
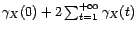 converge
en loi vers une gaussienne centrée de variance
converge
en loi vers une gaussienne centrée de variance
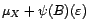 .
.
Section : Estimation de la moyenne
Précédent : Estimation de la moyenne
Suivant : Démonstration du corollaire
Thierry Cabanal-Duvillard
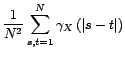
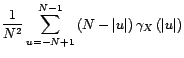

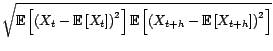
 converge aussi vers 0. Cela achève de démontrer le
point
converge aussi vers 0. Cela achève de démontrer le
point 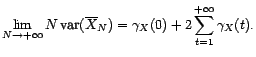 . On peut donc appliquer le théorème de convergence
dominée, et en déduire
. On peut donc appliquer le théorème de convergence
dominée, et en déduire