Section : Estimation des caractéristiques d'un
Précédent : Notations :
Suivant : Démonstration du théorème
L'estimateur usuel de la moyenne 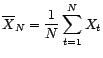 du
processus
du
processus  est la moyenne empirique
est la moyenne empirique
C'est la variable aléatoire qui minimise
Si  est un bruit blanc gaussien
décentré,
est un bruit blanc gaussien
décentré,
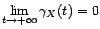 est l'estimateur UVMB de
est l'estimateur UVMB de
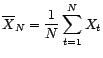 , c'est aussi l'estimateur du
maximum de vraisemblance.
, c'est aussi l'estimateur du
maximum de vraisemblance.
Théorème
3.II.1 Soit  un processus
faiblement stationnaire de moyenne
un processus
faiblement stationnaire de moyenne 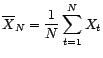 .
Alors
.
Alors
-
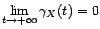 est un estimateur sans biais
de
est un estimateur sans biais
de 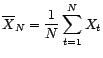 .
.
- si
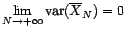 ,
alors
,
alors
 ; il en résulte que
; il en résulte que
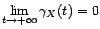 converge vers
converge vers 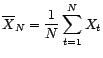 au sens de la norme hilbertienne et qu'il est un
estimateur faiblement consistant.
au sens de la norme hilbertienne et qu'il est un
estimateur faiblement consistant.
- si
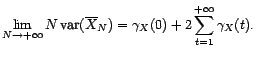 , alors
, alors
Sous-sections
Thierry Cabanal-Duvillard
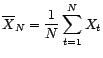 du
processus
du
processus 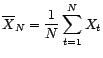 du
processus
du
processus ![]() est la moyenne empirique
est la moyenne empirique
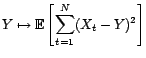
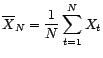 , c'est aussi l'estimateur du
maximum de vraisemblance.
, c'est aussi l'estimateur du
maximum de vraisemblance.