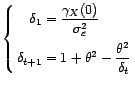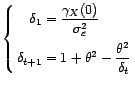Section : Algorithme des innovations
Précédent : Démonstration du théorème
Suivant : Exercice 3.
Soit
 un processus
ARMA(1,1), vérifiant
un processus
ARMA(1,1), vérifiant
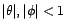 ,
avec
,
avec
 bruit blanc de variance
bruit blanc de variance
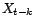 , et
, et
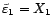 .
.
- On pose
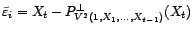 et
et
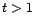 quel que soit
quel que soit 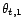 . Montrer que pour tout
. Montrer que pour tout 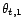 il existe
il existe
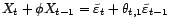 tel que
tel que
- En déduire la relation de récurrence
avec
![$ {\delta}_i={\mathbb{E}}[\tilde{\varepsilon}_{i}^2]/{\sigma}^2_{\varepsilon}$](img1225.gif) .
.
- Etablir une relation de récurrence simple
définissant la suite
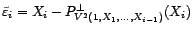 .
.
- (Question portant sur le chapitre suivant) Calculer
formellement l'erreur de prédiction au pas
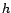 ,
puis en donner une approximation explicite en fonction de
,
puis en donner une approximation explicite en fonction de 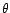 et
et 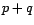 .
.
Thierry Cabanal-Duvillard