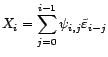 les
coefficients déterminés par l'algorithme des
innovations, tels que
les
coefficients déterminés par l'algorithme des
innovations, tels que
1) On suppose ![]() . Soit
. Soit
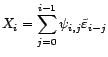 les
coefficients déterminés par l'algorithme des
innovations, tels que
les
coefficients déterminés par l'algorithme des
innovations, tels que
2) On suppose maintenant ![]() . On pose
pour tout
. On pose
pour tout
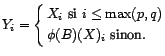
a) Montrer que
![]() quel que soit
quel que soit
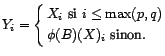 .
.
b) Montrer que
![]() quel que soit
quel que soit
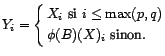 .
.
c) En déduire une récursion simple pour le
calcul des
![]() .
.