Section : Algorithme des innovations
Précédent : Remarque.
Suivant : Exercice 2.
En vertu de la stationnarité faible de 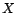 ,
il est facile de vérifier l'égalité :
,
il est facile de vérifier l'égalité :
Or
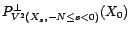 .
D'après le corollaire
.
D'après le corollaire ![[*]](file:/usr/share/latex2html/icons/crossref.gif) ,
on en déduit que
,
on en déduit que
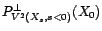 converge au sens de la norme hilbertienne vers
converge au sens de la norme hilbertienne vers
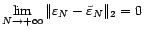 quand
quand 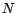 tend vers l'infini. On en déduit le premier
point, à savoir
Les deux autres limites en découlent, car
tend vers l'infini. On en déduit le premier
point, à savoir
Les deux autres limites en découlent, car
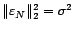 a
même limite que
a
même limite que
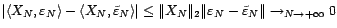 ;
d'autre part,
d'où il résulte que
converge vers
;
d'autre part,
d'où il résulte que
converge vers
En pratique, le procédé d'orthonormalisation de
Schmidt permet le calcul par récurrence de
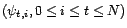 et de
et de
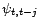 :
:
avec
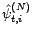 . Cette
méthode porte en statistique des processus le nom
d'algorithme des innovations. En remplaçant dans
l'algorithme précédent la fonction d'autocovariance
. Cette
méthode porte en statistique des processus le nom
d'algorithme des innovations. En remplaçant dans
l'algorithme précédent la fonction d'autocovariance
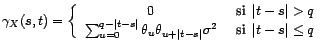 par son estimateur
par son estimateur
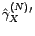 , on définit les
estimateurs
, on définit les
estimateurs
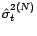 et
et
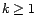 .
.
Théorème 3.II.7 Si 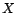 est un processus ARMA, dont l'innovation
est un processus ARMA, dont l'innovation
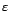 est un bruit blanc au sens
fort, possédant un moment d'ordre 4, alors, en reprenant les
notations précédentes, pour tout
est un bruit blanc au sens
fort, possédant un moment d'ordre 4, alors, en reprenant les
notations précédentes, pour tout  et pour toute suite d'entiers positifs
et pour toute suite d'entiers positifs
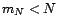 telle que
telle que 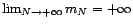 ,
,
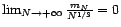 et
et
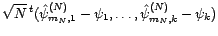 , le vecteur
aléatoire
converge en loi vers un vecteur gaussien centré de
matrice de covariance
, le vecteur
aléatoire
converge en loi vers un vecteur gaussien centré de
matrice de covariance
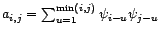 telle que
telle que
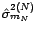 . De
plus,
. De
plus,
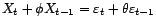 converge en
probabilité vers
converge en
probabilité vers
 .
.
Section : Algorithme des innovations
Précédent : Remarque.
Suivant : Exercice 2.
Thierry Cabanal-Duvillard
![]() ,
il est facile de vérifier l'égalité :
,
il est facile de vérifier l'égalité :![]() et de
et de
![]() :
: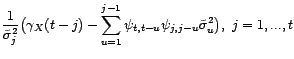

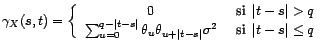 par son estimateur
par son estimateur