Section : Projecteurs orthogonaux
Précédent : Projecteurs orthogonaux
Suivant : Exemples :
Soit
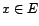 un espace
préhilbertien.
un espace
préhilbertien.
- Deux vecteurs
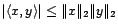 sont dits
orthogonaux si leur produit scalaire est nul.
sont dits
orthogonaux si leur produit scalaire est nul.
- Soit
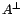 . L'orthogonal de
. L'orthogonal de 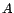 , noté
, noté 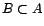 , est l'ensemble des
vecteurs de
, est l'ensemble des
vecteurs de 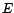 orthogonaux à tous les
éléments de
orthogonaux à tous les
éléments de 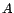 . C'est un
sous-espace vectoriel fermé de
. C'est un
sous-espace vectoriel fermé de 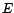 . Si
. Si
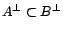 , alors
, alors
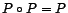 .
.
- Un endomorphisme
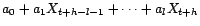 de
de 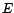 est
appelé projecteur linéaire s'il vérifie
est
appelé projecteur linéaire s'il vérifie
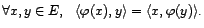 . Il est
caractérisé par son noyau (la direction de la
projection) et son image (le sous-espace sur lequel on projette),
qui sont des sous-espaces vectoriels supplémentaires.
Restreint à son image, c'est l'identité.
. Il est
caractérisé par son noyau (la direction de la
projection) et son image (le sous-espace sur lequel on projette),
qui sont des sous-espaces vectoriels supplémentaires.
Restreint à son image, c'est l'identité.
- Un endomorphisme
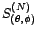 de
de 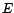 est dit auto-adjoint si et seulement si
est dit auto-adjoint si et seulement si
Théorème
5.II.1
- Soit
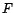 une partie fermée, convexe, non vide
d'un espace de Hilbert
une partie fermée, convexe, non vide
d'un espace de Hilbert 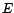 . Alors, pour tout
. Alors, pour tout 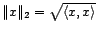 , il existe un unique point
, il existe un unique point  tel que
On note ce point
tel que
On note ce point
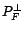 . L'application
. L'application 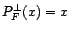 est appelée projection orthogonale sur
est appelée projection orthogonale sur
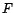 . C'est une application contractante. Quel
que soit
. C'est une application contractante. Quel
que soit 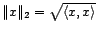 ,
,
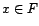 si et seulement si
si et seulement si 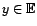 .
.
- Si
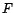 est un sous-espace vectoriel fermé
de
est un sous-espace vectoriel fermé
de 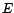 , alors
, alors 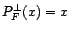 est une
application linéaire de
est une
application linéaire de 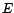 sur
sur 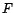 .
Pour tout
.
Pour tout 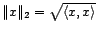 ,
,
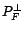 est l'unique
élément
est l'unique
élément
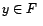 tel que
tel que
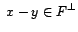 et et 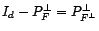 |
(51) |
Corollaire 5.II.2
Avec les mêmes notations :
- Si
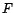 est un sous-espace vectoriel fermé
de
est un sous-espace vectoriel fermé
de 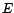 , alors
, alors 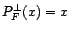 est un
projecteur auto-adjoint, dit aussi projecteur orthogonal. De plus,
est un
projecteur auto-adjoint, dit aussi projecteur orthogonal. De plus,
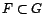 .
.
- Si
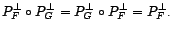 sont deux sous-espaces
vectoriels fermés de
sont deux sous-espaces
vectoriels fermés de 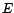 , alors
, alors
- Soit
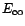 une famille
croissante de sous-espaces de Hilbert. On note
une famille
croissante de sous-espaces de Hilbert. On note
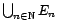 l'espace vectoriel
engendré par
l'espace vectoriel
engendré par
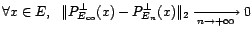 et
fermé pour la norme hilbertienne. Alors,
et
fermé pour la norme hilbertienne. Alors,
Section : Projecteurs orthogonaux
Précédent : Projecteurs orthogonaux
Suivant : Exemples :
Thierry Cabanal-Duvillard