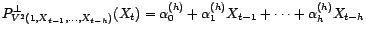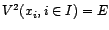Section : Projecteurs orthogonaux
Précédent : Définitions :
Suivant : Bases
hilbertiennes, et diagonalisation
- Soit
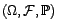 un espace de
probabilité, et
un espace de
probabilité, et
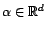 des variables
aléatoires réelles. Alors le projecteur orthogonal de
des variables
aléatoires réelles. Alors le projecteur orthogonal de
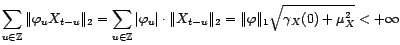 sur
sur
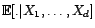 est l'espérance
conditionnelle
est l'espérance
conditionnelle
![$ {\mathbb{E}}[.\vert X_1,\ldots,X_d]$](img1709.gif) :
:
![$\displaystyle \forall Y\in L^2({\Omega},{\cal F},\P),\ \ P^\bot_{L^2(X_1,\ldots,X_d)}(Y)={\mathbb{E}}[Y\vert X_1,\ldots,X_n]\ \P$](img1710.gif)
-p.s.
![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) du
théorème
) du
théorème ![[*]](file:/usr/share/latex2html/icons/crossref.gif) :
:
-
![$ {\mathbb{E}}[Y\vert X_1,\ldots,X_d]$](img1711.gif) est
est
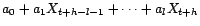 -p.s. une fonction de carré
intégrable de
-p.s. une fonction de carré
intégrable de
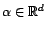 , et appartient donc à
, et appartient donc à
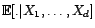 ;
;
- quel que soit
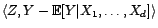 ,
,
Donc
![$ Y-{\mathbb{E}}[Y\vert X_1,\ldots,X_d]$](img1717.gif) appartient à l'orthogonal de
appartient à l'orthogonal de
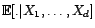 .
.
- Si
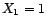 et
et 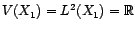 , alors
, alors
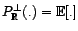 , et
, et
![$ P^\bot_{{\mathbb{R}}}(.)={\mathbb{E}}[.]$](img1721.gif) .
.
- Soient
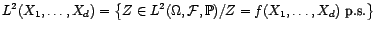 un
un 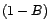 -uplet
de variables aléatoires de carré intégrable,
et
-uplet
de variables aléatoires de carré intégrable,
et
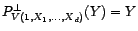 quelconque.
Alors
quelconque.
Alors
-
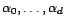 si et ssi
il existe
si et ssi
il existe
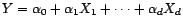 tels que
tels que
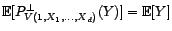 .
.
-
![$ {\mathbb{E}}[P^\bot_{V(1,X_1,\ldots,X_d)}(Y)]={\mathbb{E}}[Y]$](img1726.gif) car
car
-
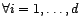
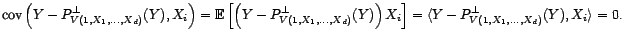 , car
, car
-
![$ P^\bot_{V(1,X_1,\ldots,X_d)}(Y)={\mathbb{E}}[Y]$](img1731.gif) si et ssi
si et ssi
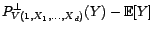 . En effet,
. En effet,
il en résulte :
Section : Projecteurs orthogonaux
Précédent : Définitions :
Suivant : Bases
hilbertiennes, et diagonalisation
Thierry Cabanal-Duvillard
![$ {\mathbb{E}}[Y\vert X_1,\ldots,X_d]$](img1711.gif) est
est
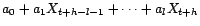 -p.s. une fonction de carré
intégrable de
-p.s. une fonction de carré
intégrable de
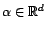 , et appartient donc à
, et appartient donc à
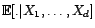 ;
;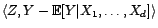 ,
,![$\displaystyle \langle Z,Y-{\mathbb{E}}[Y\vert X_1,\ldots,X_d]\rangle$](img1713.gif)
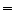
![$\displaystyle {\mathbb{E}}\left[f(X_1,\ldots,X_d)\left(Y-{\mathbb{E}}[Y\vert X_1,\ldots,X_d]\right)\right]$](img1714.gif)
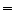
![$\displaystyle {\mathbb{E}}\left[f(X_1,\ldots,X_d){\mathbb{E}}\left[Y-{\mathbb{E}}[Y\vert X_1,\ldots,X_d]\vert X_1,\ldots,X_d\right]\right]$](img1715.gif)
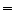
![$\displaystyle {\mathbb{E}}\left[f(X_1,\ldots,X_d)\times 0\right]=0$](img1716.gif)
![$ Y-{\mathbb{E}}[Y\vert X_1,\ldots,X_d]$](img1717.gif) appartient à l'orthogonal de
appartient à l'orthogonal de
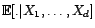 .
.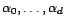 si et ssi
il existe
si et ssi
il existe
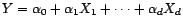 tels que
tels que
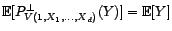 .
.![$ {\mathbb{E}}[P^\bot_{V(1,X_1,\ldots,X_d)}(Y)]={\mathbb{E}}[Y]$](img1726.gif) car
car
![$\displaystyle {\mathbb{E}}[P^\bot_{V(1,X_1,\ldots,X_d)}(Y)]=P^\bot_{V(1)}\circ P^\bot_{V(1,X_1,\ldots,X_d)}(Y)=P^\bot_{V(1)}(Y)={\mathbb{E}}[Y]. $](img1727.gif)
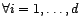
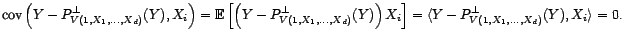 , car
, car
![$\displaystyle \mathop{\hbox{\upshape {cov}}}\nolimits \left(Y-P^\bot_{V(1,X_1,\... ...)}(Y)\right)X_i\right]=\langle Y-P^\bot_{V(1,X_1,\ldots,X_d)}(Y),X_i\rangle=0. $](img1730.gif)
![$ P^\bot_{V(1,X_1,\ldots,X_d)}(Y)={\mathbb{E}}[Y]$](img1731.gif) si et ssi
si et ssi
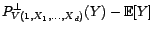 . En effet,
. En effet,![$\displaystyle P^\bot_{V(1,X_1,\ldots,X_d)}(Y)-{\mathbb{E}}[Y]$](img1733.gif)
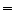
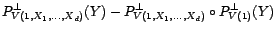
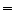
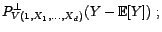
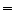
![$\displaystyle P^\bot_{V(1,X_1,\ldots,X_d)}(Y-{\mathbb{E}}[Y])\ ;$](img1736.gif)
![$\displaystyle P^\bot_{V(1,X_1,\ldots,X_d)}(Y)-{\mathbb{E}}[Y]=0$](img1737.gif)
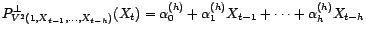
![$\displaystyle Y-{\mathbb{E}}[Y]\in Ker(P^\bot_{V(1,X_1,\ldots,X_d)})$](img1738.gif)
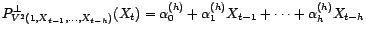
![$\displaystyle Y-{\mathbb{E}}[Y]\in V(1,X_1,\ldots,X_d)^\bot$](img1739.gif)
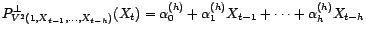
![$\displaystyle {\mathbb{E}}[1(Y-{\mathbb{E}}[Y])]={\mathbb{E}}[X_i(Y-{\mathbb{E}}[Y])]=0\ \ \forall i=1,\ldots,d$](img1740.gif)