Section : Martingales
Précédent : Premiers exemples
Suivant : Définition:
Sur l'espace filtré
 , on se
donne pour
, on se
donne pour
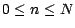 :
:
- une suite
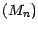 adaptée à (
adaptée à (
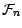 )
)
- une suite prévisible
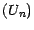
Introduisons d'autre part la notation suivante : si
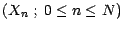 est une suite de
v.a.r. , on désignera par
est une suite de
v.a.r. , on désignera par
 la suite des
accroissements de (
la suite des
accroissements de (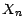 ) définie par
On peut reconstituer (
) définie par
On peut reconstituer (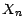 ) connaissant la suite de
ses accroissements et sa valeur initiale : on a de manière
évidente ,
) connaissant la suite de
ses accroissements et sa valeur initiale : on a de manière
évidente ,
 |
(3.2) |
On notera qu'une suite adaptée 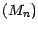 est une
martingale si et seulement si
est une
martingale si et seulement si
![$\displaystyle \textbf{E}[\Delta M_n\vert {\cal F}_{n-1}]=0\;\; \forall n\geq 1$](img557.gif)
|
(3.3) |
Sous-sections
Jacques Azéma
![]() , on se
donne pour
, on se
donne pour
![]() :
: