Section : Martingales
Précédent : Premières propriétés
Suivant : Transformées de martingales
- Sommes de v.a.r. centrées indépendantes :
Soit (
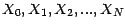 ) une suite de v.a.r.
centrées indépendantes ; posons
) une suite de v.a.r.
centrées indépendantes ; posons
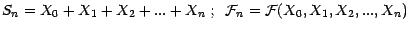 ; je dis que
; je dis que 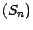 est une martingale , en effet ,
puisque
est une martingale , en effet ,
puisque 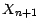 est indépendante de
est indépendante de
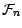 ,
Supposons de plus les v.a.
,
Supposons de plus les v.a. 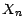 équidistribuées ; elles ont alors toutes la
même variance que nous appellerons
équidistribuées ; elles ont alors toutes la
même variance que nous appellerons 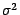 ; dans cette situation ,
; dans cette situation ,
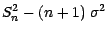 est aussi une
martingale comme le prouve le petit calcul suivant :
d'où il résulte aisément que
est aussi une
martingale comme le prouve le petit calcul suivant :
d'où il résulte aisément que
- Martingales produit: Soit (
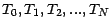 ) , une suite de v.a.
positives , indépendantes , d'espérance
) , une suite de v.a.
positives , indépendantes , d'espérance 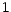 ; la suite
; la suite
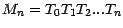 est alors une martingale
par rapport à la filtration naturelle engendrée par
les v.a.
est alors une martingale
par rapport à la filtration naturelle engendrée par
les v.a. 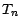 . En effet ,
. En effet ,
Il y a d'autres exemples de martingales intéressantes
associées à des suites indépendantes, mais ce
n'est pas là le plus important ; le succès de cette
théorie est dû au fait qu'elle permet d'aller
très au delà de l'indépendance : un certain
nombre de transformations simples détruisent en effet celle
ci tout en préservant la propriété de
martingale ; nous allons étudier deux d'entre elles .
Section : Martingales
Précédent : Premières propriétés
Suivant : Transformées de martingales
Jacques Azéma