Section : Définition:
Précédent : Un week-end à Monte
Suivant : Sur la
propriété de
Sur un espace filtré (
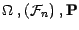 ) soient
(
) soient
(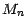 ) une martingale (resp. une sur ou une
sous-martingale) et (
) une martingale (resp. une sur ou une
sous-martingale) et (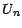 ) une suite
prévisible (resp. une suite prévisible positive) ;
) une suite
prévisible (resp. une suite prévisible positive) ;
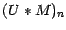 est alors une martingale (resp. une
sur ou une sous-martingale).
est alors une martingale (resp. une
sur ou une sous-martingale).
Démonstration: Bornons nous au cas des
martingales et posons
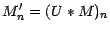 ;on a
;on a
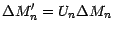 d'où , en
utilisant la prévisibilité de
d'où , en
utilisant la prévisibilité de 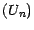 ,
,
Jacques Azéma
;on a
d'où , en utilisant la prévisibilité de
,