Section : Sur la
propriété de
Précédent : Sur la propriété de
Suivant : Temps
d'arrêt
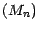 possède la
propriété de représentation prévisible
si et seulement si
possède la
propriété de représentation prévisible
si et seulement si
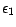 prend ses valeurs dans un
ensemble réduit à 2 points .
prend ses valeurs dans un
ensemble réduit à 2 points .
Démonstration : Soient
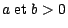 ; supposons tout
d'abord que
; supposons tout
d'abord que
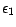 prenne ses valeurs dans
prenne ses valeurs dans 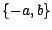 et montrons que
et montrons que 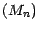 possède alors la p.r.p. ; posons
possède alors la p.r.p. ; posons
Puisque
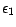 est centrée,
est centrée,
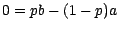 d'où
d'où
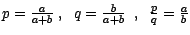 .
.
Considérons maintenant une v.a.r.
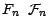 -mesurable verifiant
-mesurable verifiant
![$ \textbf{E}[F_n \vert {\cal F}_{n-1}]=0$](img590.gif) ;
nous allons montrer qu'il existe
;
nous allons montrer qu'il existe
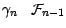 -mesurable
telle que
-mesurable
telle que
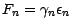 ; d'après
la proposition 2.3.2 , il existe une fonction
numérique
; d'après
la proposition 2.3.2 , il existe une fonction
numérique 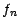 sur
sur
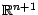 (c'est à dire une
fonction réelle de
(c'est à dire une
fonction réelle de 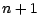 variables
réelles) telle que
variables
réelles) telle que
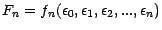 . Comme
. Comme
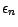 est indépendante de
est indépendante de
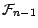 , l'espérance
conditionnelle
, l'espérance
conditionnelle
![$ \textbf{E}[F_n \vert {\cal F}_{n-1}]$](img599.gif) se
calcule à l'aide de la formule (
se
calcule à l'aide de la formule (![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) de sorte que
l'on a l'égalité
) de sorte que
l'on a l'égalité
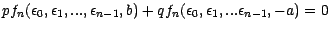 d'où l'on tire
d'où l'on tire
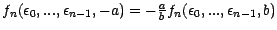 .
.
On peut alors écrire
quand on a posé
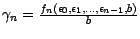 ; cela démontre notre assertion . Considérons
maintenant une martingale
; cela démontre notre assertion . Considérons
maintenant une martingale 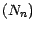 ; appliquant
ce qui précède à
; appliquant
ce qui précède à
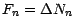 , il vient
, il vient
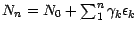 . Il
reste simplement à remarquer que
. Il
reste simplement à remarquer que 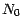 , qui est
, qui est
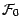 -mesurable , est une constante
réelle.
-mesurable , est une constante
réelle.
Passons à la réciproque ; posons
![$ \textbf{E}[\epsilon _1^2]=\textbf{E}[\epsilon _k^2 ]=\sigma ^2$](img613.gif) . Comme la suite
. Comme la suite
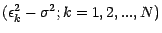 est
formée de v.a. indépendantes et centrées ,
est
formée de v.a. indépendantes et centrées ,
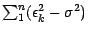 est une
martingale nulle à l'origine ; par hypothèse , il
existe une suite
est une
martingale nulle à l'origine ; par hypothèse , il
existe une suite
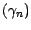 prévisible telle
que
prévisible telle
que
Il en résulte que
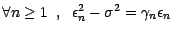 ; puisque
; puisque 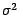 est
est 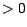 ,
cela entraîne d'abord
,
cela entraîne d'abord
 ; d'autre part
, puisque
; d'autre part
, puisque
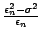 est
est
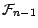 -mesurable , on
a
-mesurable , on
a
Appelant 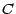 la constante figurant au
dernier membre de cette chaine d'égalités , on voit
que
la constante figurant au
dernier membre de cette chaine d'égalités , on voit
que
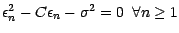 .
Il en résulte que
.
Il en résulte que
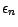 prend ses valeurs dans
l'ensemble à 2 points constitué par les racines du
trinôme
prend ses valeurs dans
l'ensemble à 2 points constitué par les racines du
trinôme
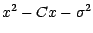 .
.
Section : Sur la
propriété de
Précédent : Sur la propriété de
Suivant : Temps
d'arrêt
Jacques Azéma
; supposons tout d'abord que
prenne ses valeurs dans
et montrons que
possède alors la p.r.p. ; posons
est centrée,
d'où
.
-mesurable verifiant
; nous allons montrer qu'il existe
-mesurable telle que
; d'après la proposition 2.3.2 , il existe une fonction numérique
sur
(c'est à dire une fonction réelle de
variables réelles) telle que
. Comme
est indépendante de
, l'espérance conditionnelle
se calcule à l'aide de la formule (
) de sorte que l'on a l'égalité
d'où l'on tire
.
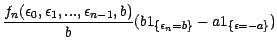
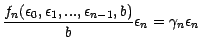
; cela démontre notre assertion . Considérons maintenant une martingale
; appliquant ce qui précède à
, il vient
. Il reste simplement à remarquer que
, qui est
-mesurable , est une constante réelle.
. Comme la suite
est formée de v.a. indépendantes et centrées ,
est une martingale nulle à l'origine ; par hypothèse , il existe une suite
prévisible telle que
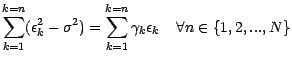
; puisque
est
, cela entraîne d'abord
; d'autre part , puisque
est
-mesurable , on a
![$\displaystyle \frac{\epsilon _n^2-\sigma ^2}{\epsilon _n}=\textbf{E}[\frac{\eps... ...sigma ^2}{\epsilon _n}]=\textbf{E}[\frac{\epsilon _1^2-\sigma ^2}{\epsilon _1}]$](img621.gif)
la constante figurant au dernier membre de cette chaine d'égalités , on voit que
. Il en résulte que
prend ses valeurs dans l'ensemble à 2 points constitué par les racines du trinôme
.