Conditionnements successifs : Soient  et
et 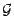 deux algèbres avec
deux algèbres avec
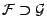 ; on a alors,
; on a alors,
quelquesoit la v.a.r. 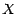 ,
,
![$\displaystyle \textbf{E}[X\vert {\cal F}\vert {\cal G}]=\textbf{E}[X\vert {\cal G}]\;\;\; ; \;\;\;\;\textbf{E}[\textbf{E}[X\vert {\cal F}]]=\textbf{E}[X]$](img438.gif)
|
(2.19) |
Il nous suffira de montrer la première
égalité ; les premiers et second membres de celle-ci
, que nous appellerons respectivement
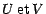 étant
étant 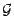 -mesurables, tout revient à montrer les
égalités
-mesurables, tout revient à montrer les
égalités
Mais
![$ \textbf{E}[U1_G]=\textbf{E}[\textbf{E}[X\vert {\cal F} ]1_G]=\textbf{E}[X1_G]$](img441.gif) , la deuxième égalite venant du fait que
, la deuxième égalite venant du fait que
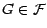 . Retenons une
conséquence pratique de ce résultat : avec les
notations de 2.3.1. , on a par exemple
. Retenons une
conséquence pratique de ce résultat : avec les
notations de 2.3.1. , on a par exemple
![]() étant
étant ![]() -mesurables, tout revient à montrer les
égalités
-mesurables, tout revient à montrer les
égalités