Section : Algèbres et partitions
Précédent : Définition:
Suivant : Exercice
Dans ce paragraphe , 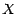 désignera une
variable aléatoire à valeurs dans
désignera une
variable aléatoire à valeurs dans 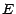 .
.
- Conditionnement par une algèbre: Soit
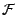 une algèbre (engendrée par une
partition
une algèbre (engendrée par une
partition 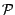 ) ; si
) ; si 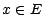 ,
on posera
(Bien noter qu'il s'agit d'égalités entre
variables aléatoires
,
on posera
(Bien noter qu'il s'agit d'égalités entre
variables aléatoires 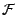 -mesurables) . Les v.a.
-mesurables) . Les v.a.
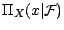 possèdent les
2 propriétés suivantes resultant immédiatement
de ce que nous avons vu en 2.3.3
possèdent les
2 propriétés suivantes resultant immédiatement
de ce que nous avons vu en 2.3.3
-
 est
est 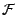 -mesurable et
-mesurable et 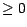
-
![$ \forall \omega \in \Omega \hspace{2cm}\sum_{x\in E}\Pi_X(x\vert {\cal F})=\textbf{E}[1_\Omega\vert {\cal F}]=1$](img467.gif)
Pour y voir plus clair, notons provisoirement 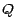 la fonction de 2 variables définie par
la fonction de 2 variables définie par
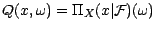 ; les
propriétés (a) et (b) s'expriment sur
; les
propriétés (a) et (b) s'expriment sur 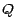 de la façon suivante:
de la façon suivante:
-
 est
est
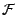 -mesurable et
-mesurable et 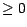
-
 est une probabilité sur
est une probabilité sur 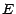
Cette fonction 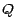 , que l'on notera
, que l'on notera
 sera appelée
loi conditionnelle de
sera appelée
loi conditionnelle de 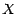 quand
quand  . On se rappellera qu'il s'agit , (cf (b)) , d'une
famille de lois de probabilité sur
. On se rappellera qu'il s'agit , (cf (b)) , d'une
famille de lois de probabilité sur 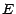 indexée par
indexée par 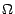
- Conditionnement par une variable aléatoire Soit
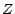 une variable aléatoire à
valeurs dans
une variable aléatoire à
valeurs dans 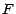 ; on supposera comme d'habitude que
; on supposera comme d'habitude que
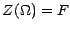 . La loi conditionnelle de
. La loi conditionnelle de
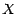 quand
quand 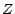 sera par
définition
sera par
définition
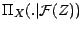 . Cet objet est
donc , comme au point 1. précédent dont nous
reprenons les notations, une fonction
. Cet objet est
donc , comme au point 1. précédent dont nous
reprenons les notations, une fonction 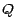 des 2
variables (x,
des 2
variables (x,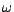 ) ; mais d'après (b) , et
compte tenu de
) ; mais d'après (b) , et
compte tenu de
2.3.2 , il existe
![$ q:E\times F\mapsto [0\;\;\; 1]$](img475.gif) telle que
telle que
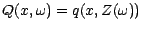 ,
, 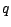 se calculant très simplement par la formule
se calculant très simplement par la formule
![$ q(x,z)=\textbf{P}[X=x\vert Z=z]$](img477.gif) ; on a donc
l'égalite
; on a donc
l'égalite
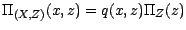 qui permet
de montrer de facon élémentaire une relation que vous
avez sans doute déjà vue dans votre jeunesse:
On peut retrouver cette formule par une voie plus abstraite , (ce
que je vous conseille de faire pour vous habituer au maniement des
espérances conditionnelles ) ; c'est une conséquence
simple de l'égalité
qui permet
de montrer de facon élémentaire une relation que vous
avez sans doute déjà vue dans votre jeunesse:
On peut retrouver cette formule par une voie plus abstraite , (ce
que je vous conseille de faire pour vous habituer au maniement des
espérances conditionnelles ) ; c'est une conséquence
simple de l'égalité
![$ \textbf{E}[f(X,Z)]=\textbf{E}[\textbf{E}[f(X,Z)\vert Z]\,]$](img480.gif) et
de (
et
de (![[*]](file:/usr/share/latex2html/icons/crossref.gif) )
.
)
.
- Lois conditionnelles et indépendance : On a vu en
(
![[*]](file:/usr/share/latex2html/icons/crossref.gif) ) que
l'indépendance d'un couple (
) que
l'indépendance d'un couple ( ) de v.a.r.
entrainait l'égalité
) de v.a.r.
entrainait l'égalité
![$ \textbf{E}[X\vert Z]=\textbf{E}[X]$](img482.gif) ; la
réciproque est grossièrement inexacte (trouver un
contre-exemple) ; il existe en revanche une condition
nécessaire et suffisante d'indépendance en termes de
loi conditionnelle ; on a le résultat suivant :
; la
réciproque est grossièrement inexacte (trouver un
contre-exemple) ; il existe en revanche une condition
nécessaire et suffisante d'indépendance en termes de
loi conditionnelle ; on a le résultat suivant :
 et
et 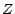 sont
indépendantes si et seulement si
sont
indépendantes si et seulement si
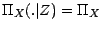
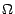 figurant
au premier membre est en réalité réduite
à la seule loi marginale de
figurant
au premier membre est en réalité réduite
à la seule loi marginale de 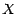 . La
démonstration de ce résultat,très simple, est
laissée au lecteur .
. La
démonstration de ce résultat,très simple, est
laissée au lecteur .
Section : Algèbres et partitions
Précédent : Définition:
Suivant : Exercice
Jacques Azéma
![]() désignera une
variable aléatoire à valeurs dans
désignera une
variable aléatoire à valeurs dans ![]() .
.![]() la fonction de 2 variables définie par
la fonction de 2 variables définie par
![]() ; les
propriétés (a) et (b) s'expriment sur
; les
propriétés (a) et (b) s'expriment sur ![]() de la façon suivante:
de la façon suivante: