Section : Algèbres et partitions
Précédent : Lois conditionnelles
Suivant : Proriétés markoviennes d'une marche
- Conditionnement d'une loi multinomiale . Soient
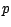 et
et 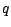 deux entiers
deux entiers
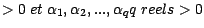 ; on pose
; on pose
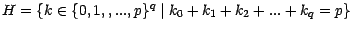 ; On dit qu'une v.a.
; On dit qu'une v.a.
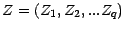 à valeurs dans
à valeurs dans
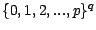 est multinomiale de
parametres
est multinomiale de
parametres
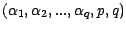 (cf
1.2.6) si elle admet pour loi la probabilité sur
(cf
1.2.6) si elle admet pour loi la probabilité sur
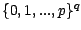 , portée par
, portée par 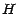 définie par
Soit
définie par
Soit 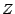 une telle variable aléatoire ;
montrer que la loi conditionnelle de (
une telle variable aléatoire ;
montrer que la loi conditionnelle de (
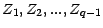 ) quand
) quand 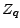 est la loi multinomiale de paramètres (
est la loi multinomiale de paramètres (
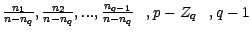 ) ; on notera que le support de cette loi conditionnelle est
aléatoire .
) ; on notera que le support de cette loi conditionnelle est
aléatoire .
- Sans titre Soit
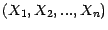 une suite de
une suite de  variables aléatoires réelles,
indépendantes, equidistribuées ; on pose
variables aléatoires réelles,
indépendantes, equidistribuées ; on pose
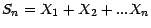 ;
;
- Soit
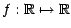 ;
montrer que
;
montrer que
![$ \textbf{E}[X_1f(S_n)]=\textbf{E}[X_2f(S_n)]=...=\textbf{E}[X_nf(S_n)]$](img488.gif)
- En déduire que
![$ \textbf{E}[X_1\vert S_n]={S_n\over n}$](img489.gif)
Jacques Azéma
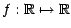 ;
montrer que
;
montrer que
![$ \textbf{E}[X_1f(S_n)]=\textbf{E}[X_2f(S_n)]=...=\textbf{E}[X_nf(S_n)]$](img488.gif)
![$ \textbf{E}[X_1\vert S_n]={S_n\over n}$](img489.gif)