Section : Le
modèle de Cox,
Précédent : L'espace des épreuves
Suivant : Lemme
:
Soit P une probabilité quelconque sur  ; examinons à quelles condiditions la suite
; examinons à quelles condiditions la suite
 est une martingale sous
P . On a
de sorte qu'une condition nécessaire et suffisante pour
qu'il en soit ainsi est :
est une martingale sous
P . On a
de sorte qu'une condition nécessaire et suffisante pour
qu'il en soit ainsi est :
![$ \textbf{E}[T_{n+1}\vert {\cal F}_n ]=1+r$](img1102.gif) ;
Il en résulte (prendre l'espérance des 2 membres) ,
que
;
Il en résulte (prendre l'espérance des 2 membres) ,
que
![$ \textbf{E}[T_n]=1+r$](img1103.gif) . Puisque
on a nécessairement
. Puisque
on a nécessairement 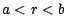 . Mais,
si le marché est viable, on peut appliquer ce qui vient
d'être dit à la probabilité P* ; ainsi :
. Mais,
si le marché est viable, on peut appliquer ce qui vient
d'être dit à la probabilité P* ; ainsi :
Une condition nécessaire pour que le
marché soit viable est :
![$ r\in ]a,b[$](img1106.gif)
;
nous supposerons cette
condition vérifiée dans toute la suite.
Il n'était pas nécessaire de recourir aux
résultats du paragraphe 3.3.4 pour obtenir ce
résultat : si l'on suppose, par exemple, 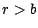 , il est facile de gagner de l'argent à coup
sûr, sans apport initial et sans risque : à l'instant
0, on emprunte une action que l'on vend immédiatement pour
placer l'argent obtenu à la caisse d'épargne (c'est
ce qu'on appelle une "vente à découvert" : on vend
une action qu'on ne possède pas), puis, à l'instant
, il est facile de gagner de l'argent à coup
sûr, sans apport initial et sans risque : à l'instant
0, on emprunte une action que l'on vend immédiatement pour
placer l'argent obtenu à la caisse d'épargne (c'est
ce qu'on appelle une "vente à découvert" : on vend
une action qu'on ne possède pas), puis, à l'instant
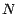 , on rachète l'action sur le
marché pour rembourser sa dette. Nous laisserons le lecteur
écrire la statégie
, on rachète l'action sur le
marché pour rembourser sa dette. Nous laisserons le lecteur
écrire la statégie  correspondante
et vérifier que l'on est en présence d'un arbitrage ;
que faire si
correspondante
et vérifier que l'on est en présence d'un arbitrage ;
que faire si 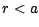 ?
?
Pour aller plus loin, nous aurons besoin du lemme suivant :
Sous-sections
Section : Le
modèle de Cox,
Précédent : L'espace des épreuves
Suivant : Lemme
:
Jacques Azéma