Section : Description du modèle .
Précédent : Description du modèle .
Suivant : Viabilité et complétude de
On pose
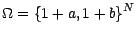 ; une
épreuve
; une
épreuve 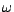 sera donc une suite
sera donc une suite
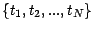 de
de 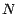 réels valant
réels valant 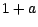 ou
ou 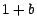 . Les fonctions coordonnées
. Les fonctions coordonnées 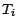 , définies par
, définies par
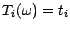 , seront les
, seront les 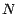 variables aléatoires centrales de ce modèle .
On notera
variables aléatoires centrales de ce modèle .
On notera
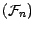 la filtration naturelle
engendrée par la suite
la filtration naturelle
engendrée par la suite 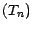 ,
complétée à l'origine par
,
complétée à l'origine par
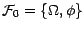 .
.
Soit
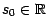 ; on définit une
suite réelle
; on définit une
suite réelle
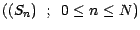 en posant
Nous laisserons au lecteur le soin de montrer que
en posant
Nous laisserons au lecteur le soin de montrer que
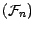 est aussi la filtration
naturelle engendrée par la suite
est aussi la filtration
naturelle engendrée par la suite 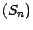 .
Rappelons que nous disposons d'une deuxième suite
.
Rappelons que nous disposons d'une deuxième suite 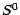 , déterministe , définie par
, déterministe , définie par
On munit  d'une probabilité
d'une probabilité
 soumise à une seule
restriction : charger tous les points de
soumise à une seule
restriction : charger tous les points de  .
.
Jacques Azéma