Section : Le
modèle de Cox,
Précédent : Le modèle de Cox,
Suivant : L'espace des épreuves
Soient 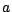 et
et  deux réels
vérifiant
deux réels
vérifiant 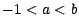 ; nous allons
construire un marché financier fini servant de modèle
mathématique à la situation boursière
simpliste suivante : il n'existe qu'un actif à risque
; nous allons
construire un marché financier fini servant de modèle
mathématique à la situation boursière
simpliste suivante : il n'existe qu'un actif à risque
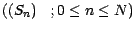 et , comme
d'habitude , un actif non risqué
et , comme
d'habitude , un actif non risqué
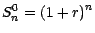 . Nos hypothèses sur
le comportement de l'action
. Nos hypothèses sur
le comportement de l'action 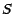 seront celles ci :
entre les instants
seront celles ci :
entre les instants  et
et 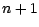 , le
cours
, le
cours 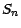 de l'actif risqué est
multiplié de façon aléatoire soit par
de l'actif risqué est
multiplié de façon aléatoire soit par 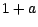 , soit par
, soit par 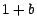 ; autrement dit ,
où
; autrement dit ,
où 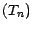 est une suite de v.a à
valeurs dans l'ensemble à deux points
est une suite de v.a à
valeurs dans l'ensemble à deux points
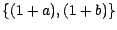 . Cette hypothèse
est très restrictive : imposer qu'un cours de bourse soit
chaque jour , ou mutiplié par 2 , ou divisé par 3 ,
apparait comme hautement irréaliste ; elle conduit
néammois à un modèle qui nous
intéressera pour 3 raisons :
. Cette hypothèse
est très restrictive : imposer qu'un cours de bourse soit
chaque jour , ou mutiplié par 2 , ou divisé par 3 ,
apparait comme hautement irréaliste ; elle conduit
néammois à un modèle qui nous
intéressera pour 3 raisons :
- il est mathématiquement très simple et permet des
calculs explicites .
- comme nous le verrons ci-dessous , c'est un marché
complet .
- il est l'analogue discret du modèle à temps
continu de Black and Scholes .
En revanche , on n'impose aucune contrainte ni sur les lois des
v.a. 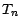 (qui peuvent dépendre de
(qui peuvent dépendre de  ) , ni sur leurs interactions (en particulier , on ne
suppose pas leur indépendance) .
) , ni sur leurs interactions (en particulier , on ne
suppose pas leur indépendance) .
Sous-sections
Section : Le
modèle de Cox,
Précédent : Le modèle de Cox,
Suivant : L'espace des épreuves
Jacques Azéma
![]() (qui peuvent dépendre de
(qui peuvent dépendre de ![]() ) , ni sur leurs interactions (en particulier , on ne
suppose pas leur indépendance) .
) , ni sur leurs interactions (en particulier , on ne
suppose pas leur indépendance) .