Section : Lemme
:
Précédent : Notations
Suivant : Prix
d'une option européenne
P* est l'unique probabilité sous laquelle la suite
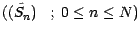 est
une martingale. Le marché de Cox, Ross et Rubinstein est
donc viable et complet.
est
une martingale. Le marché de Cox, Ross et Rubinstein est
donc viable et complet.
Démonstration :
- Vérifions tout d'abord que, sous P*,
 est une martingale ; comme
est une martingale ; comme
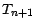 est indépendante de
est indépendante de
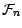 , on a
ce qui, nous l'avons vu au début de ce paragraphe, entraine
le résultat.
, on a
ce qui, nous l'avons vu au début de ce paragraphe, entraine
le résultat.
- Soit P une autre probabilité sur
 induisant la même propriété sur
la suite
induisant la même propriété sur
la suite
 ; on aura alors
; on aura alors
![$ \textbf{\^E}[T_{n+1}\vert {\cal F}_n]=1+r$](img1127.gif) ;
il résulte alors du lemme 4.3.1 que
;
il résulte alors du lemme 4.3.1 que 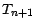 est indépendante de
est indépendante de
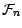 (c'est à dire de
(c'est à dire de
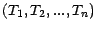 ) et a pour loi
) et a pour loi 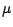 . On en déduit aisément que les v.a.
coordonnées
. On en déduit aisément que les v.a.
coordonnées 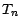 sont, sous P,
indépendantes et de loi
sont, sous P,
indépendantes et de loi 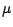 ; on a donc
P=P*, c.q.f.d.
; on a donc
P=P*, c.q.f.d.
Jacques Azéma