Section : Viabilité et complétude de
Précédent : Proposition :
Suivant : Calculs explicites
Le théorème qui suit est une conséquence
immédiate de l'étude faite au chapitre
précédent et des égalités (38)
- Théorème
- Soit
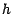 une option européenne et soit
une option européenne et soit
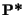 la probabilité sur
la probabilité sur  définie en 4.3.2 ; le prix
définie en 4.3.2 ; le prix 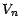 de cette option à la date
de cette option à la date  est donnée par la formule
est donnée par la formule
![$ V_n=\frac{1}{{(1+r)}^{N-n}} \textbf{E*}[h \vert {\cal F}_n]$](img1129.gif) ;
en particulier , son prix à la date 0 est
;
en particulier , son prix à la date 0 est
![$ \frac{1}{{(1+r)}^N}\textbf{E*}[h]$](img1130.gif) .
.
Beaucoup d'entre vous trouveront cette formule trop
théorique donc peu digne d'attention ; les 2
conséquences suivantes peuvent peut être les faire
changer d'avis :
- Soient
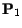 et
et
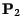 2 probabilités sur
2 probabilités sur  vérifiant respectivement
vérifiant respectivement
![$ \textbf{P}_1[T_n=1+b]=0,99 \;\;\forall n$](img1131.gif) (marché très haussier) et
(marché très haussier) et
![$ \textbf{P}_2[T_n=1+a]=0,99 \;\;\forall n$](img1132.gif) (krach permanent) ; comme
(krach permanent) ; comme
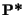 est la même dans les 2 cas
, il en sera de même du prix d'une option : contrairement
à une intuition trompeuse , le prix d'une option ne
dépend pas de la tendance du marché .On observe le
même phénomène dans le modèle de Black
and Scholes . On peut avancer l'explication suivante : dans
l'hypothèse haussière , par exemple , le vendeur
d'une option , disposant d'argent frais à l'instant 0 a la
possibilité le faire fructifier en achetant des actifs
risqués ; il peut donc se permettre de vendre son option
à un prix plus bas que celui auquel on pourrait s'attendre
.
est la même dans les 2 cas
, il en sera de même du prix d'une option : contrairement
à une intuition trompeuse , le prix d'une option ne
dépend pas de la tendance du marché .On observe le
même phénomène dans le modèle de Black
and Scholes . On peut avancer l'explication suivante : dans
l'hypothèse haussière , par exemple , le vendeur
d'une option , disposant d'argent frais à l'instant 0 a la
possibilité le faire fructifier en achetant des actifs
risqués ; il peut donc se permettre de vendre son option
à un prix plus bas que celui auquel on pourrait s'attendre
.
- La probabilité
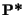 est plus simple que la
probabilité
est plus simple que la
probabilité
 gouvernant le marché ; le
fait que le prix d'une option se calcule sous
gouvernant le marché ; le
fait que le prix d'une option se calcule sous
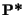 est une
bénédiction : faire des calculs avec des v.a.
indépendantes équidistribuées met tout
probabiliste dans l'état euphorique que nous allons
éprouver à la lecture du paragraphe suivant.
est une
bénédiction : faire des calculs avec des v.a.
indépendantes équidistribuées met tout
probabiliste dans l'état euphorique que nous allons
éprouver à la lecture du paragraphe suivant.
Section : Viabilité et complétude de
Précédent : Proposition :
Suivant : Calculs explicites
Jacques Azéma