Section : Viabilité et complétude de
Précédent : Viabilité et complétude de
Suivant : Notations
Soit 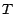 une variable aléatoire
réelle à valeurs dans l'esemble à deux points
une variable aléatoire
réelle à valeurs dans l'esemble à deux points
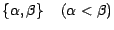 et soit
et soit 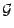 une sous algèbre de
une sous algèbre de  ;
on suppose qu'il existe une constante
;
on suppose qu'il existe une constante 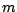 telle que
telle que
![$ \textbf{E}[T\vert {\cal G}]=m$](img1111.gif) ;
; 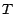 est alors indépendante de
est alors indépendante de 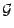 et
sa loi est donnée par les égalités
et
sa loi est donnée par les égalités
Démonstration On montre d'abord comme
précédemment que
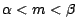 .
.
Posons
![$ A=\textbf{P}[T=\alpha\vert {\cal G}]\;\; ,\;\; B=\textbf{P}[T=\beta \vert {\cal G}]$](img1114.gif) ; en conditionnant par rapport à
; en conditionnant par rapport à 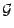 les égalités
les égalités
on obtient
Il en résulte que les variables
aléatoires  et
et 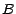 sont
solutions du système de 2 équations à 2
inconnues :
sont
solutions du système de 2 équations à 2
inconnues :
dont l'unique solution est
Il est alors important de noter que les variables
aléatoires  et
et 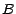 sont des
constantes ; cela signifie en effet que la loi conditionnelle de
sont des
constantes ; cela signifie en effet que la loi conditionnelle de
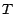 quand
quand 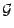 ne
dépend pas de
ne
dépend pas de 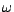 . La v.a.
. La v.a. 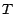 est donc indépendante de l'algèbre
est donc indépendante de l'algèbre 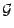 ; l'assertion concernant sa loi est à peu
près évidente .
; l'assertion concernant sa loi est à peu
près évidente .
Sous-sections
Jacques Azéma
.
; en conditionnant par rapport à
les égalités
et
sont solutions du système de 2 équations à 2 inconnues :
et
sont des constantes ; cela signifie en effet que la loi conditionnelle de
quand
ne dépend pas de
. La v.a.
est donc indépendante de l'algèbre
; l'assertion concernant sa loi est à peu près évidente .