Section : Caractérisation des processus MA
Précédent : Exercice 8.
Suivant : Preuve
du lemme .
- Montrons que
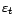 est centré :
Or l'opérateur de projection orthogonale est auto-adjoint.
D'où
Comme
est centré :
Or l'opérateur de projection orthogonale est auto-adjoint.
D'où
Comme
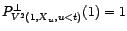 ,
,
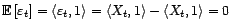 ;
d'où
Montrons maintenant que
;
d'où
Montrons maintenant que
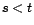 et
et
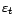 sont
décorrélées si
sont
décorrélées si 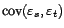 :
:
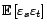
|
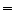 |
![$\displaystyle {\mathbb{E}}\left[{\varepsilon}_s{\varepsilon}_t\right]$](img561.gif) car les variables sont centrées
car les variables sont centrées |
|
| |
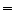 |
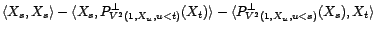 |
|
| |
 |
|
|
| |
|
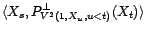
|
|
Or
On en déduit
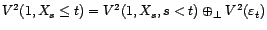 . Montrons maintenant que
. Montrons maintenant que
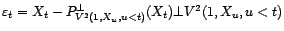 , ce dont par récurrence on peut déduire la formule
de l'énoncé.
, ce dont par récurrence on peut déduire la formule
de l'énoncé.
-
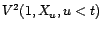 en vertu de la caractérisation de la projection orthogonale
rappelée dans la preuve du lemme
en vertu de la caractérisation de la projection orthogonale
rappelée dans la preuve du lemme ![[*]](file:/usr/share/latex2html/icons/crossref.gif) . Donc
. Donc
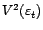 et
et
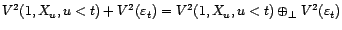 sont orthogonaux, et
sont orthogonaux, et
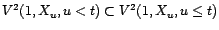 .
.
-
 et
et
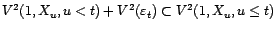 ; d'où
; d'où
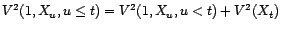 .
.
-
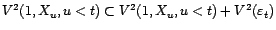 ; or
; or
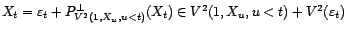 et
et
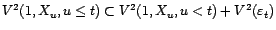 ; d'où
; d'où
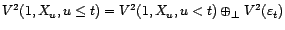 , ce qui achève de montrer que
, ce qui achève de montrer que
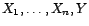 .
.
Avant de démontrer le deuxième point de la
proposition, il faut établir quelques lemmes
préliminaires.
Lemme 2.I.5 Soit
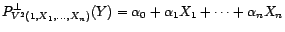 des variables
aléatoires de carré intégrable. Alors
si et seulement si
et
des variables
aléatoires de carré intégrable. Alors
si et seulement si
et
Section : Caractérisation des processus MA
Précédent : Exercice 8.
Suivant : Preuve
du lemme .
Thierry Cabanal-Duvillard