Section : Caractérisation des processus MA
Précédent : Notations.
Suivant : Exercice 8.
Soit
 un processus du
second ordre. On appelle innovation associée à
un processus du
second ordre. On appelle innovation associée à
 le processus du second ordre
le processus du second ordre
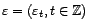 défini par
défini par
Proposition 2.I.4 Soit
 un processus du
second ordre, et
un processus du
second ordre, et
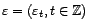 son
processus d'innovation. Alors
son
processus d'innovation. Alors
- Les variables
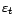 sont
décorrélées et centrées ; quel que
soient
sont
décorrélées et centrées ; quel que
soient
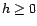
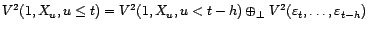 ,
on a
,
on a
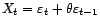 .
.
- Si
 est faiblement stationnaire, alors
est faiblement stationnaire, alors
 est un bruit blanc faible.
est un bruit blanc faible.
Thierry Cabanal-Duvillard