Section : Caractérisation des processus MA
Précédent : Preuve du théorème
Suivant : Définition :
Soit
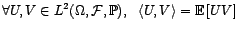 un espace
de probabilité, et
un espace
de probabilité, et
 l'espace de Hilbert des variables aléatoires de carré
intégrable, muni du produit scalaire
On note
l'espace de Hilbert des variables aléatoires de carré
intégrable, muni du produit scalaire
On note
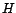 la norme hilbertienne
associée. Si
la norme hilbertienne
associée. Si 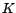 et
et 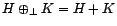 sont
deux sous-espaces de Hilbert orthogonaux, on note
sont
deux sous-espaces de Hilbert orthogonaux, on note
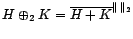 qui est un sous-espace de
Hilbert. Si
qui est un sous-espace de
Hilbert. Si 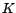 et
et 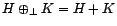 sont
supplémentaires, on note
sont
supplémentaires, on note
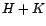 le sous-espace de Hilbert engendré par
le sous-espace de Hilbert engendré par 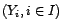 .
.
Soit
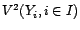 une famille de variables
aléatoires de carré intégrable,
définies sur
une famille de variables
aléatoires de carré intégrable,
définies sur
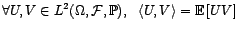 . On note
. On note
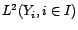 (resp.
(resp.
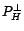 ) le sous-espace de Hilbert
de
) le sous-espace de Hilbert
de
 engendré par les combinaisons linéaires de
engendré par les combinaisons linéaires de
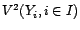 (resp. par les fonctions de
carré intégrable de
(resp. par les fonctions de
carré intégrable de
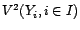 ).
).
Si 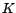 est un sous-espace de Hilbert d'un espace
de Hilbert
est un sous-espace de Hilbert d'un espace
de Hilbert 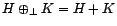 , on note
, on note 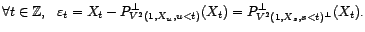 le
projecteur orthogonal de sur
le
projecteur orthogonal de sur 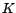 , qui est un
opérateur linéaire auto-adjoint sur
, qui est un
opérateur linéaire auto-adjoint sur 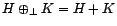 .
.
Thierry Cabanal-Duvillard
![]() une famille de variables
aléatoires de carré intégrable,
définies sur
une famille de variables
aléatoires de carré intégrable,
définies sur
![]() . On note
. On note
![]() (resp.
(resp.
![]() ) le sous-espace de Hilbert
de
) le sous-espace de Hilbert
de
![]() engendré par les combinaisons linéaires de
engendré par les combinaisons linéaires de
![]() (resp. par les fonctions de
carré intégrable de
(resp. par les fonctions de
carré intégrable de
![]() ).
).![]() est un sous-espace de Hilbert d'un espace
de Hilbert
est un sous-espace de Hilbert d'un espace
de Hilbert ![]() , on note
, on note ![]() le
projecteur orthogonal de sur
le
projecteur orthogonal de sur ![]() , qui est un
opérateur linéaire auto-adjoint sur
, qui est un
opérateur linéaire auto-adjoint sur ![]() .
.