Section : Caractérisation des processus MA
Précédent : Caractérisation des processus MA
Suivant : Notations.
Si  est un processus MA(
est un processus MA(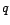 ), alors
on a déjà vu, lors de la preuve de la
propriété
), alors
on a déjà vu, lors de la preuve de la
propriété ![[*]](file:/usr/share/latex2html/icons/crossref.gif) , qu'il est
faiblement stationnaire, centré, et que sa fonction
d'autocovariance vaut
où
, qu'il est
faiblement stationnaire, centré, et que sa fonction
d'autocovariance vaut
où
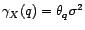 avec
avec
 bruit blanc de variance
bruit blanc de variance
 . En particulier,
. En particulier,
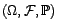 n'est pas
nul, car par hypothèse
n'est pas
nul, car par hypothèse
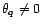 . Ce qui achève de
montrer la première implication du théorème.
. Ce qui achève de
montrer la première implication du théorème.
La démonstration de la réciproque est
repoussé après l'introduction et l'étude du
processus d'innovation.
Thierry Cabanal-Duvillard