Section : Définition et premières
propriétés
Précédent : Remarque.
Suivant : Preuve
de la propriété
Soit
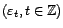 une
famille de variables aléatoires indépendantes de loi
une
famille de variables aléatoires indépendantes de loi
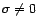 (i.e. un bruit blanc
gaussien) avec
(i.e. un bruit blanc
gaussien) avec
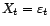 . On pose
. On pose
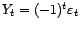 et
et
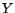 .
.
Les processus  ,
, 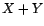 et
et 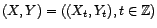 sont-ils stationnaires ? Qu'en est-il de
sont-ils stationnaires ? Qu'en est-il de
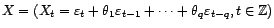 ?
?
Propriété
2.I.1 Soit  un processus
MA(
un processus
MA(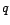 ) vérifiant
avec
) vérifiant
avec
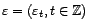 un bruit
blanc. Alors
un bruit
blanc. Alors  est faiblement (resp. fortement)
stationnaire si
est faiblement (resp. fortement)
stationnaire si
 est un bruit blanc faible
(resp. fort).
est un bruit blanc faible
(resp. fort).
Thierry Cabanal-Duvillard
![]() ,
, ![]() et
et ![]() sont-ils stationnaires ? Qu'en est-il de
sont-ils stationnaires ? Qu'en est-il de
![]() ?
?